• Складність алгоритмів
  • 14.1. Асимптотичні оцінки складності
  • 14.2. Класи складності

Складність алгоритмів

Створення та реалізація алгоритму відповідно до свого призначення визначає його складність. Проте не існує інтегрованого показника складності алгоритму, хоча існує спеціальний навіть розділ – метрична теорія алгоритмів, що займається саме проблемами складності. Інтуїтивно можна виділити такі основні складові складності алгоритму:

1. Логічна складність - кількість людино-місяців, витрачених на створення алгоритму.

2. Статична складність - довжина опису алгоритмів (кількість операторів).

3. 3. Тимчасова складність - час виконання алгоритму.

4. Ємнісна складність - кількість умовних одиниць пам'яті, необхідних для роботи алгоритму.

Головною метою теорії складності є забезпечення механізму класифікації алгоритмів за складністю. Складність алгоритму дозволяє визначитися з вибором ефективного алгоритму серед існуючих, що побудовані для розв’язання конкретної проблеми. А саме вибір серед уже існуючих алгоритмів дозволяє не розглядати логічну та статичну складність, а оцінювати ті ресурси, що знадобляться під час реалізації обраних алгоритмів.

Означення. Складність алгоритму – це кількісна характеристика, що відображує споживані алгоритмом ресурси під час свого виконання.

Основними ресурсами, що оцінюються, є час виконання і простір пам’яті.

Інтуїтивно це поняття досить зрозуміле. В алгоритму є вхід - опис завдання, яке потрібно вирішити. На його розв’язання алгоритм витрачає певний час (тобто кількість операцій). Складність - це функція від довжини входу, значення якої дорівнює максимальному (за будь-якими входами даної довжини) кількості операцій, необхідних алгоритму для отримання відповіді.

Приклад 14.1. Нехай дана послідовність з нулів та одиниць і нам потрібно з'ясувати, чи є там хоч одна одиниця. Яку складність матиме алгоритм розв’язання цієї задачі?

Розв’язання. Нехай n – кількість символів в послідовності. Алгоритм буде послідовно перевіряти, чи немає одиниці в поточному місці заданої послідовності, а потім рухатися далі, поки вхід не скінчиться. Оскільки одиниця дійсно може бути тільки одна, для отримання точної відповіді на це питання в гіршому випадку доведеться перевірити всі n символів входу. В результаті отримуємо складність порядку cn, де c  кількість кроків, що потрібна для перевірки поточного символа і переходу до наступного. Оскільки такого роду константи сильно залежать від конкретної реалізації, математичного сенсу вони не мають, і їх зазвичай ховають за символом O(О-велике) : в даному випадку фахівець із теорії складності визначив би, що алгоритм має складність

O (n) ( про символіку складності див. 14.1); іншими словами, він лінійний.

Існує і продовжує розширюватися клас варіантів поняття складності: складність знизу, зверху й у середньому, алгебраїчна складність, мультиплікативна складність, бітова складність, фундаментальні асимптотичні оцінки складності, оцінка алгоритмів за їх належністю до класів складності самих проблем, що вони розв’язують, і т. д.

 

14.1. Асимптотичні оцінки складності

Одним зі спрощених видів аналізу складності алгоритмів, що використовують при комп’ютерній їх реалізації, є асимптотичний аналіз алгоритмів. Він використовується з метою порівняння витрат часу та інших ресурсів різноманітними алгоритмами, призначеними для вирішення одного і того самого завдання. Досліджуючи зростання часу роботи алгоритму при вхідних даних досить великих розмірів, ми тим самим вивчаємо асимптотичну ефективність алгоритмів. Це означає, що нас цікавить тільки те, як час роботи алгоритму зростає зі збільшенням розміру вхідних даних, коли цей розмір збільшується до нескінченності. Зазвичай алгоритм, більш ефективний в асимптотичному сенсі, буде більш продуктивним для всіх вхідних даних, за винятком дуже маленьких. Нижче перелічені основні оцінки складності.

Позначення, що вводяться для опису асимптотичної поведінки часу роботи алгоритму, використовують функції, область визначення яких  множина невід'ємних цілих чисел N = {0,1,2, ...}. Подібні позначення зручні для опису часу роботи T(n) в найгіршому випадку як функції, визначеної тільки для цілих чисел, що становлять розмір вхідних даних.

Означення. Функція складності алгоритму f(n) має оцінку Θ(тета) й записується як f(n) = Θ(g(n)), якщо існує невід’ємна функція g(n) та додатні n₀, с₁, с₂ такі, що

c₁g(n) ≤ f(n) ≤ c₂g(n),                                                      (14.1)

при n > n₀ .

У такому разі говорять, що функція g(n) є асимптотично точною оцінкою функції f(n), оскільки за визначенням функція f(n) не відрізняється від функції g(n) з точністю до сталого множника. Важливо розуміти, що

Θ (g(n)) є не однією функцією, а множиною функцій для опису зростання f(n) з точністю до сталого множника. Іншими словами, функція f(n) належить множині Θ (g(n)), якщо існують додатні с₁ та с₂ , що дозволяють обмежити цю функцію у рамки між функціями c₁g(n) та c₂g(n) для достаньо великих значень n.

Наприклад, для методу сортування послідовності чисел алгоритмом heapsort оцінка трудомісткості становить f(n) = Θ (nlog₂n), тобто в цьому разі g(n) = nlog₂n.

З означення f(n) = Θ (g(n)) випливає, що g(n) = Θ (f(n)).

Інтуїтивно зрозуміло, що при асимптотично точній оцінці асимптотично невід’ємних функцій, доданками нижчих порядків у них можна знехтувати, оскільки при великих n вони стають неістотними. Навіть невеликої частки доданка найвищого порядку достатньо для того, щоб перевершити доданки нижчих порядків. Таким чином, для виконання нерівностей (14.1), достатньо як с₁вибрати значення, яке дещо менше коефіцієнта при самому старшому доданку, а як с₂ значення, яке дещо більше цього коефіцієнта.

Тому коефіцієнт при старшому доданку можна не враховувати, тому що він лише змінює зазначені константи.

Приклад 14.1. Розглянемо квадратичну функцію f(n) = an² + bn + c, де a, b, c – константи, причому а > 0. Відкидаючи доданки нижчих порядків за перший та ігноруючи коефіцієнт а, одержимо f(n) = Θ (n²).

Узагалі кажучи, для будь-якого полінома p(n) маємо p(n) = Θ(n^d), де d – степінь полінома при a_d > 0. Оскільки будь-яка константа – це поліном нульового степеня, то сталу функцію можна записати як Θ(n⁰) або Θ(1).

Означення. Функція складності алгоритму f(n) має оцінку О(«О-велике») й записується як f(n) = О(g(n)), якщо існує невід’ємна функція g(n) та додатні n₀, с такі, що

0 ≤ f(n) ≤ cg(n),                                              (14.2)

при n > n₀ .

Означення. Функція складності алгоритму f(n) має оцінку Ω(«омега-велике») й записується як f(n) = Ω(g(n)), якщо існує невід’ємна функція g(n) та додатні n₀, с такі, що 0 ≤, cg(n) ≤ f(n) (14.3)

при n > n₀ .

О ̶ позначення застосовуються, коли необхідно вказати верхню межу функції з точністю до сталого множника. В позначеннях теорії множин Θ(g(n)) [TEX]\subset [/TEX] O(g(n)). Оскільки О-позначення описують верхню межу, то в ході їх використання для обмеження часу роботи алгоритму в найгіршому випадку ми отримуємо верхню межу цієї величини для будь-яких вхідних даних. Таким чином, асимптотична оцінка О (n²) для часу роботи алгоритму у найгіршому випадку застосовна для часу виконання завдання з будь-якими вхідними даними, чого не можна сказати про Θ-позначення. Наприклад, оцінка в Θ(n²) для часу сортування вставками в найгіршому випадку не придатна для довільних вхідних даних. Наприклад, якщо вхідні елементи, що подаються на сортування, вже відсортовані в потрібному порядку , час роботи алгоритму сортування вставкою оцінюється як Θ(n).

Оскільки Ω - позначення використовуються для визначення нижньої межі часу роботи алгоритму в найкращому випадку, то вони визначають нижню межу часу роботи алгоритму при довільних вхідних даних. Наприклад, час роботи алгоритму сортування вставками знаходиться в межах між Ω(n) та O(n²), тобто між лінійною та квадратичною функціями від n.

На рис. 14.1 графічно подані введені вище позначення.

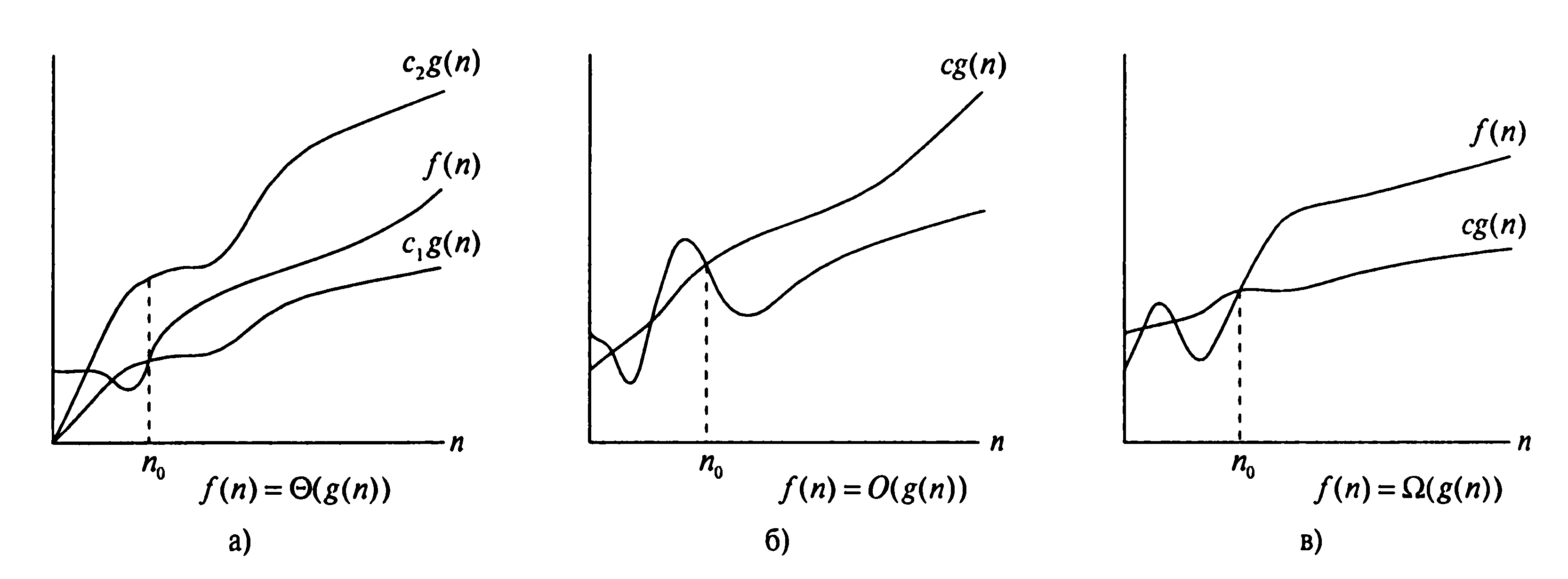
Рисунок 14.1 – Графічні приклади асимптотичних позначень

Теорема 14.1. Для будь-яких двох функцій f(n) i g(n) співвідношення f(n) = Θ(g(n)) виконується тоді й тільки тоді, коли f(n)=O(g(n)) і f(n)=Ω(g(n)).

На практиці ця теорема застосовується для визначення асимптотично точної оцінки алгоритму за допомогою асимптотично верхньої та нижньої меж.

Асимптотичний аналіз алгоритмів має не лише практичне, а й теоретичне значення. Так, наприклад, доведено, що всі алгоритми сортування, ґрунтуються на попарному порівнянні елементів, відсортують n елементів за час, не менший Ω(nlog₂n).

 

14.2. Класи складності

На початку 1960-х років, у зв'язку з початком широкого використання обчислювальної техніки для вирішення практичних завдань, виникло питання про межі практичної застосовності цього алгоритму розв'язання задачі в сенсі обмежень на її розмірність. Які завдання можуть бути вирішені на ЕОМ за реальний час? Відповідь на це питання була дана у працях Кобмена (Alan Cobham, 1964) та Едмнодса (Jack Edmonds, 1965), де були введені класи складності задач.

У теорії алгоритмів класами складності називаються множини обчислювальних задач, приблизно однакових за складністю обчислення. Говорячи більш вузько, класи складності - це множини предикатів (функцій, які отримують на вхід слово і повертають відповідь 0 або 1), що використовують для обчислення ресурси приблизно однакової кількості.

У рамках класичної теорії здійснюється класифікація завдань за класами складності (P-складні, NP-складні, експоненціально складні та ін.).

Кожен клас складності (у вузькому сенсі) визначається як множина предикатів, що мають деякі властивості. Типове визначення класу складності має такий вигляд.
     Означення. Класом складності X називається множина предикатів P (x), що обчислюються на машинах Тюрінга і використовуються для обчислення

O (f (n)) ресурсу, де n - довжина слова x.

Як ресурси зазвичай береться час обчислення (кількість робочих тактів машини Тюрінга) або робоча зона (кількість використаних осередків на рядку під час роботи). Мови, які розпізнаються предикатами з деякого класу (тобто множини слів, на яких предикат повертає 1), також називаються мовами, що належать до того самого класу. Класи прийнято позначати прописними літерами. Доповнення до класу C (тобто клас мов, доповнення яких належать C) позначається co-C.

Для кожного класу існує категорія задач, які є «найскладнішими». Це означає, що будь-яка задача з класу зводиться до такої задачі, і до того ж сама задача лежить у класі. Такі задачі називають повними задачами для даного класу. Найбільш відомими є NP-повні задачі. Повні задачі - хороший інструмент для доведення рівності класів. Достатньо для однієї такої задачі подати алгоритм, що розв’язує її і належить більш маленькому класу, і рівність буде доведено.

Розглянемо найбільш відомі класи складності задач.

1. Клас P (задачі з поліноміальною складністю).

Формальне визначення. Алгоритм ототожнюється з детермінованою машиною Тюрінга, яка обчислює відповідь при даному на вхідний рядок слові із вхідного алфавіту ∑. Час роботи алгоритму T_M(x) при фіксованому вхідному слові x визначається кількістю робочих тактів машини Тюрінга від початку до зупинки машини.

Складністю функції f: ∑* → ∑*, що обчислюється деякою машиною Тюрінга, називається функція C: N → N, що залежить від довжини вхідного слова і дорівнює максимуму часу роботи машини за всіма вхідними словами фіксованої довжини :

.                                                                                                                                                     (14.4)

Означення. Якщо для функції f існує машина Тюрінга M така, що

C_M (n) <n ^c для деякого числа c і досить великих n, то кажуть, що вона належить класу P, або поліноміальна за часом.

Тобто, задача називається поліноміальною (належить до класу P), якщо існують константа k та алгоритм, що розв’язує задачу з F_a(n)=O(n^k), де n - довжина входу алгоритму в бітах n = |D| .

Згідно з тезою Черча - Тюрінга будь-який мислимий алгоритм можна реалізувати на машині Тюрінга. Для будь-якої мови програмування можна визначити клас P подібним чином (замінивши у визначенні машину Тюрінга на реалізацію мови програмування). Якщо компілятор мови, на якому реалізований алгоритм, уповільнює виконання алгоритму поліноміально (тобто час виконання алгоритму на машині Тюрінга менший деякий за многочлен від часу виконання його на мові програмування), то визначення класів P для цієї мови і для машини Тюрінга збігаються.

Більш вузьке визначення. Іноді під класом P мають на увазі більш вузький клас функцій, а саме клас предикатів (функцій f: ∑ * → {0, 1 }). У такому разі мовою L, що розпізнає даний предикат, називається множина слів, на яких предикат дорівнює 1. Мовами класу P називаються мови, для яких існують предикати, що їх розпізнають, класу P. Очевидно, що якщо мови L₁і L₂ належать класові P, то і їх об'єднання, перетин та доповнення також належать класові P.

Задачі класу P - це, інтуїтивно, задачі, розв'язувані за реальний час. Відзначимо такі переваги алгоритмів із цього класу:

• для більшості задач із класу P константа k менше 6;

• клас P інваріантний за моделлю обчислень (для широкого класу моделей);

• клас P має властивість природної замкненості (сума або добуток поліномів є поліном).

Таким чином, задачі класу P є уточненням визначення «практично розв'язної» задачі. Прикладами завдань із класу P є цілочислове додавання, множення, ділення, одержання залишку від ділення, множення матриць, з'ясування зв'язності графів і деякі інші.

2. Клас NP (поліноміальної перевірки).

Клас NP складається із задач, розв’язання яких можна перевірити протягом поліноміального часу. Мається на увазі, що якщо ми одержимо якимось чином розв’язок деякої задачі цього класу, то протягом часу, який буде поліноміально залежати від розміру вхідних даних задачі , можна перевірити коректність такого розв’язку.

Означення. ∀ D∈D_A , |D| = n поставимо у відповідність сертифікат S∈S_A, такий, що | S | = O (n^l), та алгоритм A_S = A_S(D, S), такий, що видає «1», якщо розв’язок правильний, і «0» , якщо розв’язок неправильний. Тоді задача належить до класу NP, якщо F (A_S) = O (n^m).

Еквівалентне визначення можна отримати, використовуючи поняття недетермінованої машини Тюрiнга (тобто такої машини Тюрiнга, у програми якої можуть існувати різні рядки з однаковою лівою частиною).

Означення. Мова належить до класу NP (недетермінованих поліноміальних), якщо вона розпізнається недетермінованою машиною Тюрінга з поліноміальною часовою складністю T(n).

Отже, основна відмінність класів P і NP та, що до класу P належить задачі, які можуть бути розв’язані за час, що поліноміально залежить від об'єму початкових даних, за допомогою детермінованої обчислювальної машини (наприклад, машини Тюрінга), а до класу NP — задачі, які можуть бути розв’язані за поліноміально виражений час за допомогою недетермінованої обчислювальної машини, тобто машини, наступний стан якої не завжди однозначно визначається попередніми. Роботу такої машини можна представити як процес, що розгалужується на кожній неоднозначності: задача вважається розв’язаною, якщо хоча б одна гілка процесу прийшла до відповіді. Оскільки кожна детермінована машина Тюрінга може розглядатись як недетермінована, але без вибору варіантів кроків, то клас P міститься в класі NP (P⊆NP). Оскільки клас P міститься в класі NP, приналежність того або іншого завдання до класу NP часто відображає наше поточне уявлення про способи розв’язання даної задачі й носить неостаточний характер.

До задач класу складності NP належать, наприклад, задачі: розв'язність логічного виразу, три  кольорове розфарбування графу, побудова кліки з вершин на неорієнтованому графі, задача покриття множин та інші.

У загальному випадку немає підстав вважати, що для тієї або іншої NP-задачі не може бути знайдене P-розв’язок. Питання про можливу еквівалентність класів P і NP (тобто про можливість знаходження P-розв’язку для будь-якої NP-задачі) вважається багатьма одним із основних питань сучасної теорії складності алгоритмів. Сама постановка питання про еквівалентність класів P і NP можлива завдяки введенню поняття NP-повних задач.

3. Клас NPC (NP - повні задачі)

Неформально задача належить класу NPC, якщо вона належить класу NP і є такою самою «складною», як і будь-яка задача із класу NP. NP-повні задачі складають підмножину NP-задач і відрізняються тією властивістю, що всі NP-задачі можуть бути тим або іншим способом зведені до них. З цього виходить, що якщо для NP-повної задачі буде знайдений P-розв’язок, то P-розв’язок буде знайдений для всіх задач класу NP.

Поняття NP - повноти було введене на початку 1970-х років і ґрунтується на понятті зведення однієї задачі до іншої.

Зведення може бути представлене у такий спосіб: якщо ми маємо задачу 1 та алгоритм, що розв’язує цю задачу, тобто видає правильну відповідь для всіх конкретних проблем, що становлять задачу, а для задачі 2 алгоритм розв’язання невідомий, але якщо ми можемо переформулювати (звести) задачу 2 у термінах задачі 1, то ми розв’язуємо задачу 2.

Таким чином, якщо задача 1 задана множиною конкретних проблем D_A1, а задача 2 – множиною D_A2, й існує функція f_s(алгоритм), що зводить конкретну постановку задачі 2 (d₂) до конкретної постановки задачі 1(d₁):

ƒs (d₍₂₎∈ D_A2) = d₍₁₎∈ D_A1, то задача 2 зводиться до задачі 1.

Якщо при цьому F(ƒ_s) = O(n^k), тобто алгоритм зведення належить класу P, то говорять, що задача 1 поліноміально зводиться до задачі 2.

Означення. Задача належить до класу NPC, якщо виконуються такі дві умови: по-перше, задача повинна належати до класу NP (L є NP), і, по-друге, до неї поліноміально повинні зводитися всі задачі із класу NP (Lx=< p, для кожного Lx є NP).

Виконання цього означення показане на рис. 14.2.

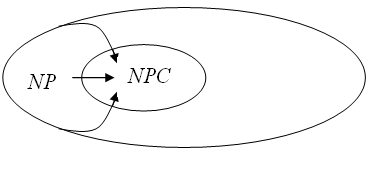
Рисунок 14.2 – Зведення і клас NPC.

Теорема 14.1. Якщо існує задача, що належить до класу NPC, для якої існує поліноміальний алгоритм розв’язання (F = O(n^k)), то клас P збігається із класом NP, тобто P=NP.

Схема доведення буде складатися зі зведення будь-якої задачі з NP до даної задачі із класу NPC з поліноміальною трудомісткістю й розв’язання цієї задачі за поліноміальний час (за умовою теореми).

У цей час доведено існування сотень NPС задач, але для жодної з них поки не вдалося знайти поліноміального алгоритму розв’язання. У цей час дослідники припускають таке співвідношення класів, що наведене на рис. 14.3, де P ≠NP і задачі із класу NPC не можуть бути розв’язані (сьогодні) з поліноміальною трудомісткістю.

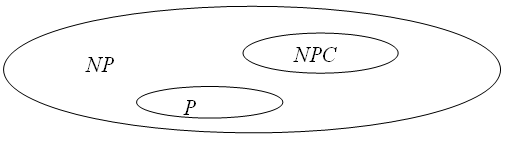
Рисунок 14.3 – Співвідношення класів P, NP, NPC.

Оскільки метод зведення базується на тому, що для деякої задачі відома її NP  повнота, то для доведення NP – повноти різних задач, нам знадобиться «перша» NP – повна задача. Як таку використовуємо задачу на здійсненність, у якій задана булева комбінаційна схема, що складається з логічних елементів ( або задано КНФ – кон’юнктивну нормальну форму). В задачі запитується, чи існує набір вхідних булевих величин, для яких на виході буде видане значення 1.

Прикладами NP-повних задач є, крім задачі про кон'юнктивну форму, задача комівояжера, розфарбування графа, задача про гамільтонів цикл у графі та інші.

4. Інші класи складності

Дослідження складності алгоритмів дозволили по-новому поглянути на розв’язання багатьох класичних математичних задач і знайти для ряду таких задач (множення многочленів і матриць, розв’язання лінійних систем рівнянь та ін.), розв’язання, що вимагають менше ресурсів, ніж традиційні.

Прості класи складності визначаються такими факторами:

• типом обчислювальної задачі: найбільш часто використовуються задачі прийняття рішень.

• моделлю обчислень: найбільш поширеною моделлю обчислень є детермінована машина Тюрінга, але багато класів складності визначають на основі недетермінованої машини Тюрінга, логічних схем, квантової машини Тюрінга, монотонних схем і т.д.

• ресурсами, які мають межі: вказується як "поліноміальний час", "логарифмічний простір", "стала глибина" тощо.

Усі класи складності знаходяться в ієрархічному відношенні: одні містять у собі інші. Однак про більшість включень невідомо, чи є вони строгими. Одна з найбільш відомих відкритих проблем у цій сфері  рівність класів P і NP. На даний момент найбільш поширеною є гіпотеза про невиродженість ієрархії (тобто всі класи різні).

Наведемо приклад побудови однієї з можливих ієрархічних структур класів складності.

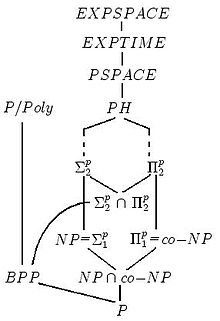
Рисунок 14.4 – Ієрархія класів складності

На цій ієрархії представлені, наприклад, такі класи, що побудовані на ймовірнісних машинах Тюрінга ( BPP ), префіксом co позначені доповнення до класів, PSPACE – клас, допустимий детермінованою машиною Тюрінга з поліноміальним обмеженим простором і т. д.