Ключові терміни:
Атом (элементарное высказывание), Высказывание, Значенние истинности, Интерпретацией высказываний, Логика высказываний, Однозначно определенным высказыванием, Правила построения формул, Проблема решения, дизъюнкцией высказываний, импликация (условное предложение), отрицание, эквиваленцияОсновные понятия логики высказываний
1.1. Основные определения
Логика как самостоятельная наука возникла в IV веке до н.э. в трудах Аристотеля, который опираясь на накопленные до него знания, дополнил их собственными и создал систему формального логического вывода, которая заключается в том, что в рассуждениях одни предложения исходят из других через определенную связь между их формой и структурой независимо от их содержания.
Революционные научные волнения конца XIX - начала ХХ века затронули и логику Аристотеля, путем реализации идеи Г. В. Лейбница , предложенной им еще в конце ХVII века , о применении в логике математической символики и построений логических исчислений . Эта идея реализована в работах Д. Буля , Ч.С. Пирса, Ф. Л. Г. Фреге , наряду со многими исследованиями других ученых.
Классическая математическая логика включает два основных раздела: логику высказываний и логику предикатов. Для их построения существуют два подхода ( языка ) , на основе которых основаны два варианта формальной логики: алгебра логики и логическое исчисление . Между основными понятиями этих языков имеет место взаимно однозначное соответствие, но строго говоря эти термины не синонимы.
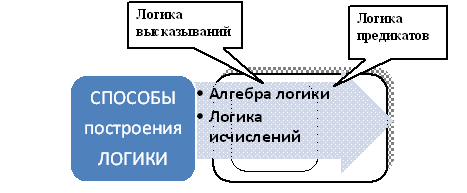
Рисунок 1.1 – Составные части классической математической логики
По своей сути логика высказываний - это наука про размышления, предпосылки и выводы которых складываются из высказываний.
Определение 1.1.1. Высказыванием называют осмысленное выражение обычного языка, которому можно приписать значения истинности.
Таким выражением может стать утверждение или повествовательное предложение, о котором можно сказать, истинное оно или ложное. Следует иметь в виду, что в логике высказываний нет средства, чтобы установить истинность или ложность простого высказывания. Если истинность и ложность нельзя установить вообще (то есть с помощью других наук), то такое высказывание не рассматривается (например: указательные высказывания, бессмысленные утверждения).
Определение 1.1.2. Значенние истинности – это абстрактный объект, которой ставится в соответтствии с высказыванием: истина – когда высказывание отвечает действительности, ложь – когда высказывание не отвечает действительности.
Обозначают : “Истина ” – И, T (True), или 1; “Ложь” – Л, F (False) або 0.
Пример 1.1.1. Определить какие из данных предложений являются выражениями:
“Днепр впадает в Черное море ”; “Днепр впадает в Азовское море ”; “Кто вы?”;
“Расстояние от Земли до Сонця равняется 150 млн км ”.
Решение. Первые два предложения являются высказываниями, причем первое является истинным, а второе – ложным высказыванием. Третье предложение не является высказыванием, поскольку оно не повествовательное. Четвертое предложение также не является высказыванием. Его истинность или ложность зависит от определенной точности.
Классическая логика высказываний оперирует только двумя значениями истинности: И и Л, но не одновременно одним и другим, поэтому ее называют двузначной или бинарной логикой.
Повествовательные предложения могут быть простыми и сложными. Каждое простое предложение может быть утверждением и не может быть разбито на более мелкие предложения.
Определение 1.1.3. Атомом (элементарным высказыванием) называется такое высказывание, которое является простым повествовательным предложением, т.е. не имеет составных частей.
Для обозначения атомо используют, как символы, буквы латинского алфавита с индексами или без них.
Сложные предложения, как правило, состоят из простых предложений, соединенных союзами. То есть простые предложения, которые представляют атомы и союзы, являются элементами словаря, необходимого для формализации естественного языка с помощью логики высказываний. Значение истинности сложного высказывания определяется значениями истинности его составных частей.
Алгебра высказываний полностью абстрагуруется от смыслового значения высказываний, принимая во внимание только их предметное значения, то есть денотат, которым выступают такие абстрактные объекты, как "истина" и "ложь".
Определение 1.1.4. Интерпретацией высказываний называют приписывание значений истинности атомам, из которых построены высказывания.
Если высказывания содержат n атомов, то можно составить 2n интерпретаций.
Определение 1.1.5. Однозначно определенным высказыванием називают высказывания, значение истинности которого не зависит от ситуации. Например, “3![]() 3=9” = И. Но существуют высказывания, которые могут принимать разные значения. Например, “Завтра будет снег”, можно придавать значение “Истина ” и “Ложь ” в зависимости от конкретной ситуации.
3=9” = И. Но существуют высказывания, которые могут принимать разные значения. Например, “Завтра будет снег”, можно придавать значение “Истина ” и “Ложь ” в зависимости от конкретной ситуации.
1.2. Высказывания и логические связки
Определение 1.2.1. Логика высказываний это алгебрагическая структура
[TEX]\langle [/TEX]{ X, I }, ![]()
![]()
![]()
![]() ,
, ![]() , ¬ ,
, ¬ , ![]() ,
,![]()
![]() ~ , X , I [TEX]\rangle [/TEX] с носителем – двоичным множеством { Л : “Ложь”, И : “Истина”}, операциями – логическими связками: “ [TEX]\wedge [/TEX] ” - конъюнкция, “ [TEX]\vee [/TEX] ” - дизъюнкция “ ¬ ”– отрицание, “
~ , X , I [TEX]\rangle [/TEX] с носителем – двоичным множеством { Л : “Ложь”, И : “Истина”}, операциями – логическими связками: “ [TEX]\wedge [/TEX] ” - конъюнкция, “ [TEX]\vee [/TEX] ” - дизъюнкция “ ¬ ”– отрицание, “ ![]() ” – импликация, “ ~ ” – эквивалентность и константами : Л – ложь и И – истина.
” – импликация, “ ~ ” – эквивалентность и константами : Л – ложь и И – истина.
В обычном языке для образования сложного предложения из простых предложений используют служебные слова – связки : “ и ”, “ или ”, “ неправильно, что” и другие. Например два предложения “ Я поеду летом к морю ” и “ Я поеду летом в горы ” можно объединить связкой “ или ” в одно сложное предложение “ Я поеду летом к морю или в горы ”. Здесь связку “ или ” нельзя присоединить ни к первому, ни ко второму простому предложению, она обслуживает одновременно оба простых предложения и поэтому называется бинарной. Например, в предложении “Неправильно, что жителей в Киеве меньше, чем во Львове ” происходит противоречие
“ В Киеве меньше жителей, чем во Львове ”. Связка “ неправильно, что … ” является унарною, потому что применяется к одному предложению. Кроме рассмотренных, существуют связки : “ если ”, “ если … то ”, “ и ”, “ тогда ”, “… тоогда и только тогда ”, “ а ”, “ нет ” и другие.
Логические связки можно рассмотреть как формальные обозначения связок, которые им соответствуют, табл. 1.2.1.
Таблиця 1.2.1
|
Название |
Обозначения |
Аналог естественного языка |
|
отрицание |
¬ |
“ нет”, “ неправильно, что” |
|
дизъюнкция |
[TEX]\vee [/TEX] |
“или” |
|
конъюнция |
[TEX]\wedge [/TEX] |
“и” |
|
импликация |
|
“ если …,то ” |
|
эквивалентность |
~ , |
“ эквивалентно”, “равносильно”, “… тогда и только тогда ”, “ если и только если” |
Операции ![]() ,
, ![]() ,
, ![]() , ~ являются бинарными логическими связками, а операция ¬ – унарной. Сложные высказывания, которые построены с простых высказываний, называют формулами или молекулами.
, ~ являются бинарными логическими связками, а операция ¬ – унарной. Сложные высказывания, которые построены с простых высказываний, называют формулами или молекулами.
Определение 1.2.2. Правила построения формул в логике высказываний определяют следующим:
-
Атом есть формула.
-
Если A и B – формулы, то A
 B, A
B, A B, A
B, A B, A~B, ¬A – также формулы.
B, A~B, ¬A – также формулы. -
Никаких формул, кроме порожденных указанными выше правилами не существует.
Формулы логики высказываний, которые соответствуют сложным высказываниям, принимают значения И и Л в зависимости от значений элементарных высказываний и логических связок, из каких они построены.
Формулы логики высказываний удобно представлять таблицами истинности, которые представляют значение истинности формулы в зависимости от последовательного перебора все возможных значений истинности простых высказываний, которые составляют формулу (см. табл. 1.2.2.)
Таблиця 1.2.2
|
A |
B |
¬A |
A |
A |
A |
A~B |
|
Л |
Л |
И |
Л |
Л |
И |
И |
|
Л |
И |
И |
Л |
И |
И |
Л |
|
И |
Л |
Л |
Л |
И |
Л |
Л |
|
И |
И |
Л |
И |
И |
И |
И |
Из таблицы истинности следует, что отрицание ¬A истинно тогда и только тогда, когда высказывание A ложно. Эта унарная операция отвечает отрицанию в обычном языке, которое может иметь разные синтаксические выражения, наприкмер, предложение “ Неправильно, что у Руслана есть машина ” равнозначно предложению “ У Руслана нет машины”.
Выражение A![]() B называют конъюнкцией высказывания A и B, которое истинно тогда и только тогда, когда истинны оба высказывания A и B. Эта логическая операция соответствует в естественной языке связке “ и ”, что соединяет два предложения.
B называют конъюнкцией высказывания A и B, которое истинно тогда и только тогда, когда истинны оба высказывания A и B. Эта логическая операция соответствует в естественной языке связке “ и ”, что соединяет два предложения.
Пример 1.2.1. Записать в виде формулы логики высказывания и определить истинное значение таких высказываний:
1. “ 8 делится на 4 и 8 больше 6 ”;
2. “ 8 делится на 4 и 7 больше 8 ”.
Решение. В данных высказываниях выделим атомы. Их три:
A – “ 8 делится на 4 ”,
B – “ 8 больше 6 ”,
C – “ 7 больше 8 ”.
Тогда высказывание 1 будет отвечать формуле A![]() B, а высказывание 2 – формуле A
B, а высказывание 2 – формуле A![]() С. Будем считать, что высказывание С – ложно. Используя истинное значение высказываний A, B, C определим значения высказываний 1 и 2.
С. Будем считать, что высказывание С – ложно. Используя истинное значение высказываний A, B, C определим значения высказываний 1 и 2.
A ![]() B = И
B = И ![]() И = И; A
И = И; A ![]() С = И
С = И ![]() Л = Л.
Л = Л.
Высказывание A![]() B називают дизъюнкцией высказываний A или B, которое действительно тогда и только тогда, когда истинно хотя бы одно логическое высказывание A или B. Эта логическая операция отвечает в естественном языке связке “ или ”, что соединяет два предложения.
B називают дизъюнкцией высказываний A или B, которое действительно тогда и только тогда, когда истинно хотя бы одно логическое высказывание A или B. Эта логическая операция отвечает в естественном языке связке “ или ”, что соединяет два предложения.
Пример 1.2.2. Записать в виде формулы логики высказываний и определить истинное значение таких высказываний:
1. “ 3 + 2 = 6 или 3 ![]() 2 = 6 ” ;
2 = 6 ” ;
2. “ 4 – 2 = 3 или 4 ![]() 2 = 7 ” .
2 = 7 ” .
Решение. В данных высказываниях выделим атомы:
-
A – “ 3 + 2 = 6 ” ; B – “ 3
 2 = 6 ” ;
2 = 6 ” ;
-
C – “ 4 – 2 = 3 ” ; D – “ 4
 2 = 7 ”
2 = 7 ”
-
Тогда высказывание 1 будет отвечать формуле A
 B, а высказывание 2 – формуле C
B, а высказывание 2 – формуле C D. По условию высказывание B истинное, а высказывание A, C, D ложное, поэтому : A
D. По условию высказывание B истинное, а высказывание A, C, D ложное, поэтому : A 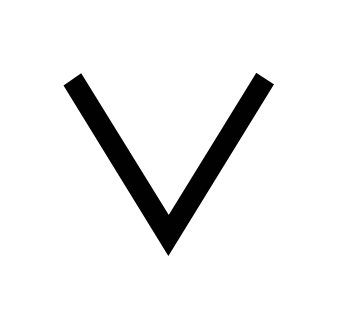 B = Л
B = Л 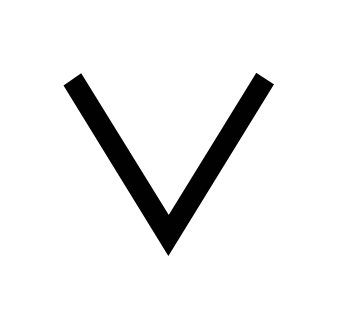 И = И; C
И = И; C 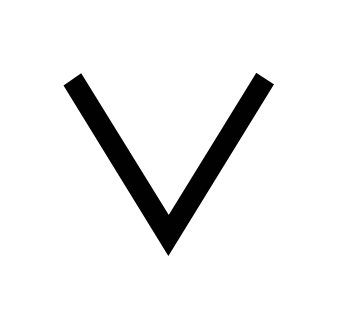 D = Л
D = Л 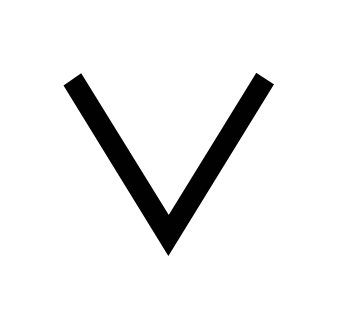 Л = Л.
Л = Л.
Пример 1.2.3. Пусть заданы высказывания: A – “ Николай любит играть в футбол ”; B – “ Николай любит играть в волейбол ”; С – “ Николай любит играть в теннис ”. Необходимо записать высказывание “ Николай любит играть в футбол и неправильно, что он любит играть в волейбол или теннис ” в виде формулы логики высказываний и построить соответственно ей таблицу истинности.
Решение. Высказывание “ Николай любит играть в волейбол или теннис ” можно записать в виде формулы логики высказываний как B![]() C. Высказывания “Неправильно, что он любит играть в волейбол или теннис ” может быть записано в виде формулы логики высказываний ¬( B
C. Высказывания “Неправильно, что он любит играть в волейбол или теннис ” может быть записано в виде формулы логики высказываний ¬( B![]() C ), поскольку отрицание применимо ко всему высказыванию, которое следует после связки “ что … ”. Исходя из этого, исходная форма сложного логического высказывания будет иметь вид A
C ), поскольку отрицание применимо ко всему высказыванию, которое следует после связки “ что … ”. Исходя из этого, исходная форма сложного логического высказывания будет иметь вид A![]() ¬( B
¬( B![]() C ).
C ).
Таблиця истинности такого высказывания приведена в табл. 1.2.3.
Таблиця 1.2.3
|
A |
B |
C |
B |
¬( B |
A |
|
Л |
Л |
Л |
Л |
И |
Л |
|
Л |
Л |
И |
И |
Л |
Л |
|
Л |
И |
Л |
И |
Л |
Л |
|
Л |
И |
И |
И |
Л |
Л |
|
И |
Л |
Л |
Л |
И |
И |
|
И |
Л |
И |
И |
Л |
Л |
|
И |
И |
Л |
И |
Л |
Л |
|
И |
И |
И |
И |
Л |
Л |
Из таблицы истинности сложного высказывания следует, что в том случае данное логическое высказывание истинно, когда высказывание A – истинно, а высказывание B и C – ложны.
1.3. Условные и эквивалентные высказывания
Из талицы истинности, табл. 1.2.2, следует, что высказывание A![]() B, что представляет собой импликацию (условное предложение), принимает значение ложности тогда и только тогда, когда A - истинно, а B - ложно. В созданном предложении A
B, что представляет собой импликацию (условное предложение), принимает значение ложности тогда и только тогда, когда A - истинно, а B - ложно. В созданном предложении A![]() B высказывание A називают предпосылкой (условием), а B – следствием (выводом). На естественном языке причинно-следственные связи между высказываниями A и B описывают такими оборотами: “ Если A, то B ”, “A является достаточным основанием для B” и так далее.
B высказывание A називают предпосылкой (условием), а B – следствием (выводом). На естественном языке причинно-следственные связи между высказываниями A и B описывают такими оборотами: “ Если A, то B ”, “A является достаточным основанием для B” и так далее.
Пример 1.3.1. Для высказывания “ Если идет дождь, то чтобы не промокнуть я открываю зонтик над головой” записать формулу высказываний и построить таблицу истинности.
Решение. Для данного высказывания введем атомы :
A – “ идет дождь ”, B – “ чтобы не промокнуть я открываю зонтик над головой ”.
Тогда данному высказыванию будет соответствовать формула A![]() B, а результаты интерпретации данного высказывания приведены в таблице истинности, табл. 1.3.1.
B, а результаты интерпретации данного высказывания приведены в таблице истинности, табл. 1.3.1.
Таблиця 1.3.1
|
A |
B |
A |
Результат |
|
Л |
Л |
И |
останусь сухим |
|
Л |
И |
И |
останусь сухим |
|
И |
Л |
Л |
намокну |
|
И |
И |
И |
останусь сухим |
С помощью имплікации можно формально выразить понятия достаточного и необходимого условия. Например, если A![]() B, то это обозначает, что “A есть достаточным условием для B ” и одновременно, что “ B есть необходимым условием для А ”. То есть необходимость для А можно записать в форме “В только, если А” - A
B, то это обозначает, что “A есть достаточным условием для B ” и одновременно, что “ B есть необходимым условием для А ”. То есть необходимость для А можно записать в форме “В только, если А” - A![]() B. удверждение “А является необходимым и достаточным условием для В” эквивалентно двойной импликации
B. удверждение “А является необходимым и достаточным условием для В” эквивалентно двойной импликации ![]() .
.
Покажем это с помощью таблицы истинности, табл. 1.3.2.
Таблиця 1.3.2
|
|
|
|
|
|
|
Л |
Л |
И |
И |
И |
|
Л |
И |
И |
Л |
Л |
|
И |
Л |
Л |
И |
Л |
|
И |
И |
И |
И |
И |
Из таблицы истинности замечаем, что высказывание ![]() истинно тогда и только тогда, когда высказывания
истинно тогда и только тогда, когда высказывания ![]() и
и ![]() истинны или ложны одновременно, что и отвечает эквиваленции.
истинны или ложны одновременно, что и отвечает эквиваленции.
Но не при всех условных высказываниях бывает так.
Пример 1.3.2. В высказывании “ Если число n парное (![]() ), то n делиться нацело на 4 (
), то n делиться нацело на 4 (![]() ) ” показать необходимость и достаточность условий и записать её истинность через знак импликации.
) ” показать необходимость и достаточность условий и записать её истинность через знак импликации.
Решение. Поскольку ни одно непарное число на 4 не делится, то это условие ![]() является необходимой, но в то же время есть парные числа которые не деляться нацело на 4, например 10. То есть, очевидным является отсутствие достаточности условия в заданном высказывании. Поэтому заданное высказывание по условию
является необходимой, но в то же время есть парные числа которые не деляться нацело на 4, например 10. То есть, очевидным является отсутствие достаточности условия в заданном высказывании. Поэтому заданное высказывание по условию ![]() ложно, а правильной импликацией для заданного условия будет
ложно, а правильной импликацией для заданного условия будет ![]() .
.
Пример 1.3.3. В высказывании “ Если геометрическая фигура-квадрат (![]() ), то она прямоугольник, у которого все стороны равны между собой (
), то она прямоугольник, у которого все стороны равны между собой (![]() ) ” показать необходимость и достаточность условия и записать его через знак логической связки.
) ” показать необходимость и достаточность условия и записать его через знак логической связки.
Решение. По условию квадрат (![]() ) – это прямоугольник, у которого все стороны равны между собой (
) – это прямоугольник, у которого все стороны равны между собой (![]() ), что является необходимым и достаточным условием для выполнения
), что является необходимым и достаточным условием для выполнения ![]() и поэтому логической связью между данными высказываниями будет эквиваленция
и поэтому логической связью между данными высказываниями будет эквиваленция ![]() .
.
С условным высказыванием ![]() связаны еще три высказывания: конверсия, инверсия и контрапозиция. Они определеяются таким образом:
связаны еще три высказывания: конверсия, инверсия и контрапозиция. Они определеяются таким образом:
![]() – конверсия высказывания
– конверсия высказывания ![]() ;
;
¬![]() ¬
¬![]() – инверсия высказывания
– инверсия высказывания ![]() ;
;
¬![]() ¬
¬![]() – контрапозиция высказывания
– контрапозиция высказывания ![]() .
.
Пример 1.3.4. Для высказывания “ Если он хорошо играет в футбол, то он популярный ” найти конверсию, инверсию и контрапозицию.
Решение. В соответствии с их определениями, искомые результаты будут иметь такое содержание.
Конверсия – “ Если он популярный, то он хорошо играет в футбол ”.
Инверсия – “ Если он не хорошо играет в футбол, то он не популярный ”.
Контрапозиция – “ Если он не популярный, то он не хорошо играет в футбол ”.
Определение 1.3.1. Высказывание ![]() ~
~![]() називают эквивалентностью (эквиваленцией) тогда и только тогда, когда высказывание
називают эквивалентностью (эквиваленцией) тогда и только тогда, когда высказывание ![]() и
и ![]() ложны или истинны одновременно. Эта операция отвечает в естественном языке оборотам:
ложны или истинны одновременно. Эта операция отвечает в естественном языке оборотам:
“ тогда и только тогда, когда”, “ для того, чтобы ”, “ необходимо и достаточно”.
Из таблицы истинности, табл. 1.3.1., следует, что выражение ![]() ~
~![]() эквивалентно выражению
эквивалентно выражению ![]() . Это свидетельствует про то, что логическая эквивалентность изображает импликацию в обеих направлениях. Исходя из определения эквивалентности формула для нее имеет следующий вид(¬[TEX]A\sim B=(A\wedge B)\vee A\wedge[/TEX]¬В).
. Это свидетельствует про то, что логическая эквивалентность изображает импликацию в обеих направлениях. Исходя из определения эквивалентности формула для нее имеет следующий вид(¬[TEX]A\sim B=(A\wedge B)\vee A\wedge[/TEX]¬В).
Пример 1.3.5. Записать в виде формулы логики высказываний и определить истинное значение таких высказываний.
1. “Для того чтобы 4 : 2 = 2, необходимо и достаточно, чтобы 4 - 2 = 2 ”.
2. “ 4 : 2 = 3 равнозначно 4 - 2 = 1 ”.
Решение. Вводим обозначение атомов:
A = 4 : 2 = 2 ; B = 4 - 2 =2 ;
C = 4 : 2 = 3 ; D = 4 - 2 = 1.
Тогда можно сказать, что высказыывание 1 отвечает формуле ![]() ~
~![]() , а высказывание 2 – формуле
, а высказывание 2 – формуле ![]() ~
~![]() . Если атомы
. Если атомы ![]() и
и ![]() истинны, а атомы
истинны, а атомы ![]() и
и ![]() ложны, то высказывание истинности значений сложных высказываний следующее:
ложны, то высказывание истинности значений сложных высказываний следующее:
![]() ~
~ ![]()
![]() И ~ И = И;
И ~ И = И; ![]() ~
~ ![]() = Л ~ Л = И.
= Л ~ Л = И.
Чтение формул сложных высказываний может быть неознозначным, если не ввести скобки, которые указывают, в каком порядке связываются между собой символы. Последовательность выполнения (приоретет операций в логике высказываний является следующей - ¬, ![]() ,
, ![]() ,
, ![]() , ~ .
, ~ .
Например, такие выражения без скобок равны формулам со скобками
![]() ;
; ![]() ~
~![]() ~
~![]() .
.
В логике высказываний любую ее формулу можно поставить в соответствие какому-то сложному высказыванию естественной формы и наоборот. Для того, чтобы щоб преобразовать сложное предложение в формулу логики высказываний необходимо выполнить следующие шаги алгоритма.
1.Путем анализа сложного предложения определить является ли оно сокращенным.
2. Если предложение сокращенное, то следует его заменить полным вариантом.
3. В полном варианте выделить простые предложения и взять их в скобки, оставив за скобками служебные слова.
4. Процесс взятия в скобки повторять до тех пор, пока полностью все сложное предложение не окажется взятым в скобки.
5. Заменить союзы и обороты естественного языка соответствующими логическими связями, а простые предложения атомарными формулами.
Пример 1.3.6. Предложение “ Поскольку я лег поздно спать, я проспал и поэтому не пошел на работу ” записать в виде формулы логики высказываний.
Решение. В этом сложном предложении выделим простые предложения и возьмем их в скобки “ Поскольку ( я лег поздно спать ), ( я проспал ) и поэтому не ( пошел на работу ) ”.
Все три простые предложения связаны служебными словами, которые выражают логические отношения, а перед третьим предложением стоит частица “ не ”, что отвечает логической операции “ отрицание ”. Поскольку третье предложение не является полным, то дополняем его отсутствующим подлежащим “ я ” и введем атомы:
A – “ Я лег поздно спать ”, B – “ Я проспал ”, C – “ Я пошел на работу ”.
Заменив простые предложения символами атомов, а служебные слова – логическими связками, получим формулу логики высказываний
![]() ¬С.
¬С.
1.4. Интерпретация формул логики высказываний
Приписывание значений И или Л атомарным формулам, которые входят в сложные формулы, називают интерпретацией.
Все формулы логики высказываний разделяются на тождественно истинные, тождественно ложные и нейтральные.
Определение 1.4.1. Формулу называют тождественно истинной (тавтологией или общезначимой), если она принимает значение “ Истина ” на всех интерпретациях (наборах значений переменных).
Например, высказывание “ Он пойдет или не пойдет в магазин ” является тавтологией, поскольку или одно высказывание, или другое обязательно состоится.
Пример 1.4.1. С помощью таблицы истинности определить истинность значения формулы логики высказывания
![]() .
.
Решение. Строим таблицу истинности для заданой формулы логики высказываний, табл. 1.4.1.
Таблиця 1.4.1
|
|
|
|
|
|
|
Л |
Л |
И |
Л |
И |
|
Л |
И |
И |
Л |
И |
|
И |
Л |
Л |
Л |
И |
|
И |
И |
И |
И |
И |
Из таблицы истинности вытекает, что заданное высказывание является “ Истинным ” на всех четырех возможных наборах переменных этого высказывания, поэтому оно является тавтологией.
Пример 1.4.2. Доказать, если высказывание ![]() и
и ![]() тавтологии, то
тавтологии, то ![]() тоже тавтология.
тоже тавтология.
Решение. По условию ![]() и
и ![]() – тавтологии. Пусть при некотором распределении значений истинности для пропозиционных переменных, которые входят в
– тавтологии. Пусть при некотором распределении значений истинности для пропозиционных переменных, которые входят в ![]() и
и ![]() ,
, ![]() принимает значение “Ложность”. Но поскольку
принимает значение “Ложность”. Но поскольку ![]() есть тавтология, то при том же распределении значений истинности
есть тавтология, то при том же распределении значений истинности ![]() приобретает значение “Истинно”. Тогда высказывание
приобретает значение “Истинно”. Тогда высказывание ![]() получает значение “Ложность”, но это является противоречием, потому, что
получает значение “Ложность”, но это является противоречием, потому, что ![]() есть тавтология.
есть тавтология.
Определение 1.4.2. Формулу називают тождественно ложной (противоречивой или неосуществимой), если она приобретает значение “ Ложность” на всех интерпретациях (наборах значений переменных).
Например, высказывание “ Она двигается в направлении школы и она не двигается в направлении школы ” является противоречивым, так как невозможно одновременно делать и то и другое. То есть это высказывание является тождественно ложным.
Пример 1.4.3.С помощью таблицы истинности определить является ли тождественно ложной формула ![]() ¬
¬![]() ¬
¬![]() .
.
Решение. Строим таблицу истинности для заданной формулы логического высказывания, табл. 1.4.2.
Таблиця 1.4.2
|
|
|
|
¬ |
¬ |
¬ |
|
|
Л |
Л |
И |
И |
И |
Л |
Л |
|
Л |
И |
И |
И |
Л |
И |
Л |
|
И |
Л |
Л |
Л |
И |
И |
Л |
|
И |
И |
И |
Л |
Л |
И |
Л |
Из таблицы истинности выплывает, что высказывание заданное формулой принимает значение “ Ложность” на всех четырех возможных наборах переменных этого высказывания, то есть является тождественно ложным.
Определение 1.4.3. Формулу називают нейтральной (необщезначимой или непротиворечивой), если она на одних интерпритациях приобретает значение “Истина”, а на других “ Ложность”.
Пример 1.4.4. С помощьютаблицы истинности определить является ли нейтральной формула ![]() .
.
Решение. Строим таблицу истинности за данной формулой логического высказывания, табл. 1.4.3.
Таблиця 1.4.3
|
|
|
|
|
|
|
Л |
Л |
И |
Л |
И |
|
Л |
И |
И |
И |
И |
|
И |
Л |
Л |
И |
Л |
|
И |
И |
И |
И |
И |
Из таблицы истинности выплывает, что высказывание, заданное логической формулой, приобретает при разных интерпритациях два значения “ Истина ” или “ Ложь”. Поєтому формула логического вісказівания является нейтральной.
Особенная роль в алгебре высказываний принадлежит тождественно истинным формулам, как способам правильных умозаключений, которые от истинных ссылок приводят к истинным высказываниям.
[TEX]\overline{\overline{A}}=A[/TEX] - закон двойного отрицания;
[TEX]A\vee \overline{A} [/TEX] - закон исключения третьего;
[TEX]\overline{A\wedge \overline{ A}}[/TEX] - закон отрицания противоречия;
A⇒A - закон тождественности;
[TEX]\begin{equation}\left. \begin{array}{c} A \wedge A\Leftrightarrow A \\ A\vee A\Leftrightarrow A\end{array} \right\} \end{equation}[/TEX] - закон идемпотетичности;
[TEX](A\Rightarrow B)\Leftrightarrow (\overline{B}\Rightarrow \overline{A}) [/TEX]- закон контрапозиции;
[TEX](A\Rightarrow B)\wedge (B\Rightarrow C)\Rightarrow (A\Rightarrow C)[/TEX]- закон силогизма;
[TEX]\begin{equation}\left. \begin{array}{c}\overline{A\wedge B} \Leftrightarrow\overline{A}\vee \overline{B} \\\overline{A\vee B}\Leftrightarrow \overline{A}\wedge \overline{B} \end{array} \right\} \end{equation} [/TEX]- закон де Моргана;
[TEX]A\wedge (A\Rightarrow B)\Rightarrow B[/TEX]- правило Модус поненс(modus ponens)
Для доказательства, что приведенные формулы являются тавтологией достаточно применить таблицу истинности.
Определения 1.4.4. Размышления называют правильными, если оно выражается тождественно истинной формулой.
Для проверки правильности размышления строят соответственно к нему формулу и определеяют является ли она тождественно ситинной. Истинность формулы можно проверить или с помощью таблицы истинности,где на всех интерпритациях она принимает значения “ Истина ”, или с помощью тождественных превращений, сведя их к виду одного из логических законов, где получают тоже значения “ Истина ”, что в соответствии с формулой размышлений является тавтологией.
Определения 1.4.5. Формулы алгебры высказываний α(А1, А2,…,Аn) и β(А1, А2,…,Аn) называются равносильными (логично эквивалентными), если значение истинности формулы α сохраняется со значением истинности формулы β.
1.5. Проблема решения в алгебре высказываний.
Функциональная полнота множества логических операций
Проблема решения в логике высказываний рассматривается как ответ на вопрос: а существует ли алгоритм, который за конечное число шагов дает возможность определить тип любой формулы алгебры высказываний. В алгебре высказываний эта проблема решается позитивно. В часности, можно предложить способы:
1. Составление таблиц истинности формул;
2. Применение метода размышлений от противного;
3. Сведение формул к нормальным формам.
Понятно, что таблица истинности для любой формулы от n высказынных переменных может быть построена за конечное число шагов и определит тип формулы. Но число строк таблицы (2n) может оказаться слишком большим при значительном количестве атомов, которые составляют формулу. Поэтому на практике в таком случае лучше применять метод 2 или 3.
Анализ формул с использованием метода размышлений от противного базируется на таких умозаключениях:
А) Якщо припустимо, що для деякого набору значень атомів формула α(A1, A2, …, An) приймає значення “ Хибність ”, а після аналізу формули прийдемо до протиріччя, то відносно формули α робимо висновок, що вона є тавтологією.
Б) Якщо припустимо, що для деякого набору значень атомів формула α(A1, A2, …, An) приймає значення “ Істина ” і прийдемо до протиріччя, то є суперечною.
В) Якщо не одержимо протиріччя ні при припущенні А) , ні при припущенні Б), то робимо висновок, що формула α є нейтральною.
Приклад 1.5.1. Визначити тип формули α = ((A ⇒ B) ⇒A) ⇒A.
Розв’язання. Припустимо, що α не є тотожно істинною формулою. Тоді повинен існувати такий набір значень атомів, на якому вона приймає значення “ Хибність ”. Формула α є імплікацією. Значення “ Хибність ” можливо лише за умови, що (A⇒B)⇒A приймає на цьому наборі значення “ Істина ”, а
А - “ Хибність ”. А тоді, слідує,що A⇒B повинно приймати значення “ Хибність ”, що неможливо, оскільки А - “ Хибність ”. Отже, α є тавтологією.
Перед тим, як розв’язувати проблему вирішення, інколи корисно спочатку перетворити формулу логіки висловлювань за допомогою рівносильних перетворень до деякої стандартної форми. Такими формами є диз’юнктивна нормальна форма (ДНФ) та кон’юнктивна нормальна форма (КНФ).
Зафіксуємо деяку множину Х логічних змінних.
Означення 1.5.1. Елементарною кон’юнкцією (диз’юнкцією) називається кон’юнкція ( диз’юнкція) скінченного числа попарно різних логічних змінних, взятих із запереченням або без нього.
Наприклад, ![]() є елементарними кон’юнкціями,
є елементарними кон’юнкціями, ![]() є елементарними диз’юнкціями, а
є елементарними диз’юнкціями, а ![]() або
або ![]() вже такими не будуть.
вже такими не будуть.
Означення 1.5.2. Елементарні кон’юнкції, що містять всі змінні з Х, будемо називати конституентами одиниці над Х, а елементарні диз’юнкції, які задовольняють подібну властивість – конституентами нуля над Х.
Неважко бачити, що кожна конституента одиниці (відповідно, конституента нуля) тільки на одному, єдиному для неї, наборів атомів приймає значення “Істина” (відповідно, значення “Хибність”).
Означення 1.5.3. Диз’юнктивною (кон’юнктивною) нормальною формою називається диз’юнкція (кон’юнкція) скінченого числа попарно різних елементарних кон’юнкцій (диз’юнкцій).
Наприклад, ![]() є ДНФ,
є ДНФ, ![]() - КНФ. Надалі елементарні кон’юнкції в ДНФ будемо називати доданками, а елементарні диз’юнкції в КНФ – множниками.
- КНФ. Надалі елементарні кон’юнкції в ДНФ будемо називати доданками, а елементарні диз’юнкції в КНФ – множниками.
Означення 1.5.4. ДНФ (КНФ) називається досконалою, якщо всі її доданки (множники) являють собою конституенти одиниці (нуля) над множиною всіх її атомів.
Досконалі форми будемо відповідно позначати ДДНФ та ДКНФ.
Довільну формулу алгебри висловлювань можна перетворити в одну з нормальних форм. Для цього необхідно виконати ряд кроків:
-
Усунути логічні зв’язки “Імплікація” та “Еквіваленція” за формулами
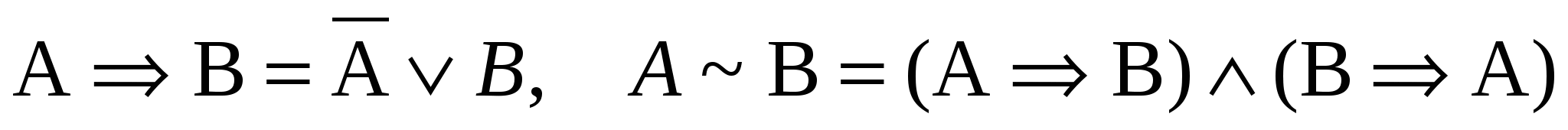 .
. -
Використати закон подвійного заперечення та закони де Моргана для перенесення знаку заперечення безпосередньо до атомів.
-
Використати відповідні закони дистрибутивності.
Приклад 1.5.2. Шляхом перетворень одержати для формули α = А ![]() В
В
рівносильні їй ДНФ та КНФ.
Рішення. ![]() - КНФ.
- КНФ.
![]() - ДНФ.
- ДНФ.
Інший шлях перетворення будь якої формули алгебри висловлювань до нормальних форм – це побудова спочатку для даної формули таблиці істинності, а потім за таблицею складаємо ДДНФ або ДКНФ.
Означення 1.5.5. Деяка множина операцій алгебри висловлювань називається функціонально повною, якщо довільна формула алгебри висловлювань рівносильна формулі, в яку входять лише операції з цієї системи.
Теорема 1.5.1. Кожна з множин операцій {![]() ,
, ![]() ,
, ![]() }, {
}, {![]() ,
, ![]() }, {
}, {![]() ,
, ![]() }, {
}, {![]() , } є функціонально повною.
, } є функціонально повною.
Доведення. Оскільки для довільних формул α і β алгебри висловлювань мають місце рівносильності:
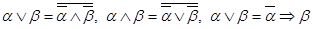 ,
,
то достатньо довести, що перша з означених в теоремі 1.5.1 множин є функціонально повною - { ![]() ,
, ![]() ,
, ![]() }, а всі інші автоматично стають функціонально повними за рівносильностями.
}, а всі інші автоматично стають функціонально повними за рівносильностями.
Формально це вже доведено, бо за алгоритмом ми зможемо перетворити будь-яку формулу алгебри висловлювань в ДНФ чи КНФ ( див. приклад 1.5.2), для сполучення атомів в яких застосовуються тільки операції з множини {![]() ,
, ![]() ,
, ![]() }. Застосуємо інше доведення, використовуючи таблиці істинності і тим самим заодно доведемо ще одну теорему.
}. Застосуємо інше доведення, використовуючи таблиці істинності і тим самим заодно доведемо ще одну теорему.
Теорема 1.5.2. Кожна функція логіки висловлювань є функцією істинності деякої ДНФ (КНФ).
Доведення. Нехай задана функція логіки висловлювань представима таблицею істинності з ![]() рядками, де кожен рядок містить деякий розподіл значень істинності для набора змінних . В кожному рядку і =
рядками, де кожен рядок містить деякий розподіл значень істинності для набора змінних . В кожному рядку і = ![]() ,
, ![]() , … ,
, … , ![]() таблиці істинності атоми і сама
таблиці істинності атоми і сама ![]() може набирати значення X або I. На наборах атомів в і-му рядку, що надають функції значення І складемо елементарну кон’юнкцію Xi1[TEX]\wedge [/TEX]Xi2[TEX]\wedge [/TEX]…[TEX]\wedge [/TEX]Xin , де Xij = Aij, якщо Aij є І,
може набирати значення X або I. На наборах атомів в і-му рядку, що надають функції значення І складемо елементарну кон’юнкцію Xi1[TEX]\wedge [/TEX]Xi2[TEX]\wedge [/TEX]…[TEX]\wedge [/TEX]Xin , де Xij = Aij, якщо Aij є І, ![]() , якщо Aij є Х. З’єднаємо всі елементарні кон’юнкції операцією диз’юнкція.
, якщо Aij є Х. З’єднаємо всі елементарні кон’юнкції операцією диз’юнкція.
Покажемо, що одержана конструкція є шуканою ДНФ.
За означенням 1.5.2. кожна конституента одиниці тільки на одному, єдиному для неї, наборів атомів приймає значення І, тобто тільки для наборів і-го рядку, а на всіх інших рядках вона прийме значення Х. Тому кожний кон’юнктивний одночлен в побудованій ДНФ надасть значення І тільки в своєму рядку. Отже, побудована таким чином ДНФ є рівносильною до функції представленою таблицею істинності і теорему 1.5.2 доведено, а одночасно доведено і теорему 1.5.1. Для побудови КНФ дії аналогічні.
Приклад 1.5.3. Утворити ДНФ та КНФ для функції логіки висловлювань, яка представлена таблицею істинності.
|
А1 |
А2 |
f |
|
X |
X |
I |
|
X |
I |
I |
|
I |
X |
I |
|
I |
I |
X |
Розв’язання. Для рядків таблиці зі значенням І для f записуємо елементарні кон’юнкції ![]() А1[TEX]\wedge [/TEX]
А1[TEX]\wedge [/TEX] ![]() А2 ,
А2 , ![]() А1 [TEX]\wedge [/TEX] А2 , А1 [TEX]\wedge [/TEX]
А1 [TEX]\wedge [/TEX] А2 , А1 [TEX]\wedge [/TEX] ![]() А2 , які зв’язуємо між собою диз’юнкцією. Одержимо ДНФ:
А2 , які зв’язуємо між собою диз’юнкцією. Одержимо ДНФ:
f = ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ).
).
КНФ для даної функції - f = ![]() А1 [TEX]\vee [/TEX]
А1 [TEX]\vee [/TEX] ![]() А2 .
А2 .
1.6. Дедуктивні висновки у логіці висловлювань
У логіці висловлювань правила висновку використовують, щоб виводити одні істинні речення з інших істинних речень. У коректному дедуктивному виведенні висновок з необхідністю випливає з посилок.
Означення 1.6.1. Логічним наслідком висловлювання ![]() є висловлювання
є висловлювання ![]() , якщо формула
, якщо формула ![]() є тотожно істинною. Це визначення може бути узагальнено для випадку
є тотожно істинною. Це визначення може бути узагальнено для випадку ![]() висловлювань, якщо
висловлювань, якщо ![]() – тотожно істинна формула.
– тотожно істинна формула.
Приклад 1.6.1. Показати, що висловлювання ![]()
![]() є логічним наслідком висловлювання [TEX]A\wedge \urcorner C[/TEX].
є логічним наслідком висловлювання [TEX]A\wedge \urcorner C[/TEX].
Розв’язання. Доведемо, що формула [TEX]A\wedge \urcorner C((A\wedge B)\vee \urcorner C)[/TEX] є загальнозначущою. Для її доведення використаємо тотожності логіки висловлювань та еквівалентні перетворення
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() I
I![]() I.
I.
Отже формула ![]()
![]()
![]()
![]()
![]()
![]()
![]() є загальнозначущою, а за означенням 1.6.1
є загальнозначущою, а за означенням 1.6.1 ![]()
![]() - логічний наслідок.
- логічний наслідок.
Означення 1.6.1. Дедуктивним висловлюванням називають висновок формули ![]() з формули
з формули ![]() , заснований на тому, що
, заснований на тому, що ![]() є логічним наслідком
є логічним наслідком ![]() .
.
Приклад 1.6.2. Довести правильність міркування за дедукцією - “ Постанова кабинету Міністрів ухвалюється, якщо за неї голосує більшість міністрів. За постанову не проголосувала більшість міністрів, тому постанова не ухвалюється ”.
Розв’язання. До речень висловлювання введемо такі атоми :
A – “ за постанову проголосувала більшість міністрів ”;
B – “ постанова ухвалюється ”; ![]() A – “ за постанову не проголосувала більшість міністрів ”;
A – “ за постанову не проголосувала більшість міністрів ”; ![]() B – “ постанова не ухвалюється ”;
B – “ постанова не ухвалюється ”;
Тоді засновки і висновки зазначимо відповідно через ![]() ~
~![]() ,
, ![]()
![]() ,
, ![]()
![]() і приєднавши за допомогою імплікації до кон’юнкції засновків
і приєднавши за допомогою імплікації до кон’юнкції засновків ![]() ~
~![]()
![]()
![]() висновок
висновок ![]()
![]() одержимо
одержимо ![]() ~
~![]()
![]()
![]()
![]()
![]() .
.
Перевіримо за допомогою таблиці істинності, табл. 1.6.1., що задана імплікація ![]() ~
~![]()
![]()
![]()
![]()
![]() є логічним наслідком.
є логічним наслідком.
Таблиця 1.6.1
|
|
|
|
|
|
|
|
|
X |
X |
I |
I |
I |
I |
I |
|
X |
I |
X |
I |
X |
X |
I |
|
I |
X |
X |
X |
I |
X |
I |
|
I |
I |
I |
X |
X |
X |
I |
Із таблиці істинності слідує, що отримано тотожно істинне висловлювання. Отже, виходячи із законів, задане по умові міркування задовольняє визначення дедуктивного висновку. Таким чином, істинність висновку в дедуктивному висновку гарантується істинністю засновків.
Твердження 1.6.1. Висловлювання ![]() є логічним наслідком висловлювання
є логічним наслідком висловлювання ![]() , якщо висловлювання
, якщо висловлювання ![]()
![]()
![]() є тотожно хибним.
є тотожно хибним.
Твердження 1.6.2. Висловлювання ![]() є логічним наслідком висловлювання
є логічним наслідком висловлювання ![]() , якщо на всіх інтерпретаціях, на яких
, якщо на всіх інтерпретаціях, на яких ![]() істинне,
істинне, ![]() теж істинне.
теж істинне.
Тотожна істинність або хибність засновків імплікації дозволяє зробити висновок про істинність або хибність наслідку.
Твердження 1.6.3 Якщо висловлювання ![]() є логічним наслідком висловлювання
є логічним наслідком висловлювання ![]() , а висловлювання
, а висловлювання ![]() – тотожно істинне висловлювання, то висловлювання
– тотожно істинне висловлювання, то висловлювання ![]() також – тотожно істинне.
також – тотожно істинне.
Твердження 1.6.4 Якщо висловлювання ![]() є тотожно хибним, то для будь-якого висловлювання
є тотожно хибним, то для будь-якого висловлювання ![]() правильно, що
правильно, що ![]()
![]() .
.
Правила для дедуктивного висновку будують на підставі загальнозначущих формул логіки висловлень виду ![]()
![]() .
.
Для наочного зображення правила умовиводів схематично записують за допомогою риски, над якою пишуть посилки, а під нею – висновок. Якщо посилок дві й більше, їх записують одну під одною ( табл. 1.6.2.)
Таблиця 1.6.2
|
Правило дедукти вного висновку |
Тавтологія |
Назва правила |
|
A_____________
|
|
Правило відділення (Modus Ponens) |
|
B→C [TEX]\overline{A\rightarrow C} [/TEX] |
|
Гіпотетичний силогізм |
|
|
|
Від’ємна форма правила відділення (Modus Tollens) |
|
|
|
Правило введення диз’юнції (правило розширення) |
|
|
|
Правило введення кон’юнції |
|
|
|
Правило видалення диз’юнції (диз’юнктивний силогізм) |
|
|
|
Правило видалення кон’юнції |
|
|
|
Правило контрапозиції імплікації |
|
|
|
Правило вибору |
|
|
|
Правило виключаючого вибору |
|
|
|
Правило зведення до абсурду (Reduction ad Absurdum) |
Правильність всіх перелічених в табл. 1.6.2 логічних висловлювань можна довести за допомогою таблиць істинності. З усіх правил, наведених в табл. 1.6.2, найбільш часто використовується правило відділення. Правило відділення має такий логічний сенс, якщо засновок правильний, то правильний і наслідок із нього.
Приклад 1.6.3. Дано висловлювання “ Якщо n ділиться на 9, то n ділиться на 3 ”. Також відомо, що “n ділиться на 9”. Який висновок можна зробити, виходячи з ціх двох висловлювань?
Розв’язання. Введемо атомарні висловлювання :
A – “ n ділиться на 9 ”,
B – “ n ділиться на 3 ”.
Висловлювання “ Якщо n ділиться на 9, то n ділиться на 3 ” можна записати у вигляді формули ![]() . З одночасного виконання засновків
. З одночасного виконання засновків ![]() і
і ![]() можна зробити висновок
можна зробити висновок ![]() за правилом відділення “ n ділиться на 3 ”.
за правилом відділення “ n ділиться на 3 ”.



