Числення висловлювань
При побудові алгебри висловлювань (розділ 1) в основу покладено поняття висловлювання, як об’єкту приймаючому логічні значення “Істина“ або “Хибність” (закон виключеного третього). Ці поняття в багатьох випадках суб’єктивні і не відносяться до математичних.
В цьому розділі розглядається формалізована аксіоматична теорія – числення висловлювань, яка вільна від указаної вище вимоги і представляє одну з можливих аксіоматизацій алгебри висловлювань.
Довільну формулу F числення висловлювань можна змістовно інтерпретувати як складене висловлювання, істинність або хибність якого залежить від істинності елементарних висловлювань, що до нього входять. Таким чином, кожній формулі F числення висловлювань можна аналогічно тому, як це було зроблено в алгебрі висловлювань, поставити у відповідність функцію істинності f.
При побудові числення висловлювань можуть бути вибрані різні системи аксіом і правила виводу, проте при будь-якому виборі множина формул числення висловлювань збігається з множиною тотожно істинних формул алгебри висловлювань.
2.1. Формальна аксіоматична теорія L
Означення 2.1.1. Формальна аксіоматична теорія L є визначеною, якщо виконані такі умови.
- 1. Задано деякий злічений алфавіт – символи теорії
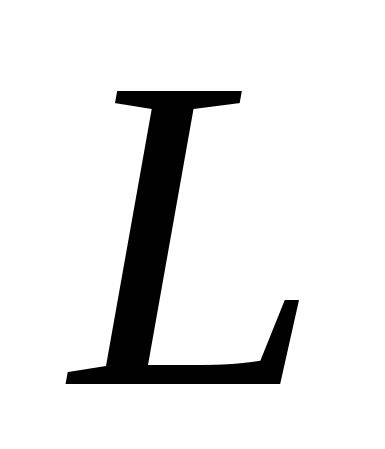 . Скінченні послідовності символів теорії
. Скінченні послідовності символів теорії 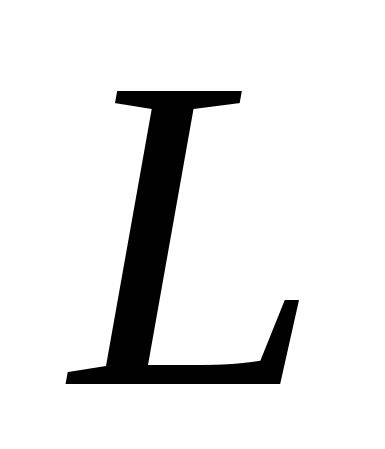 називають виразами теорії L.
називають виразами теорії L. - 2. Задано підмножину виразів теорії L, яку називають множиною формул теорії L (часто існує процедура, за допомогою якої можна завжди визначити, чи є даний вираз формулою).
- 3. Задано деяку множину формул, елементи якої називають аксіомами теорії L (якщо є можливість перевірити, чи є дана формула аксіомою, то теорію L називають ефективно аксіоматизованою, або аксіоматичною теорією).
- 4. Задано скінченну множину
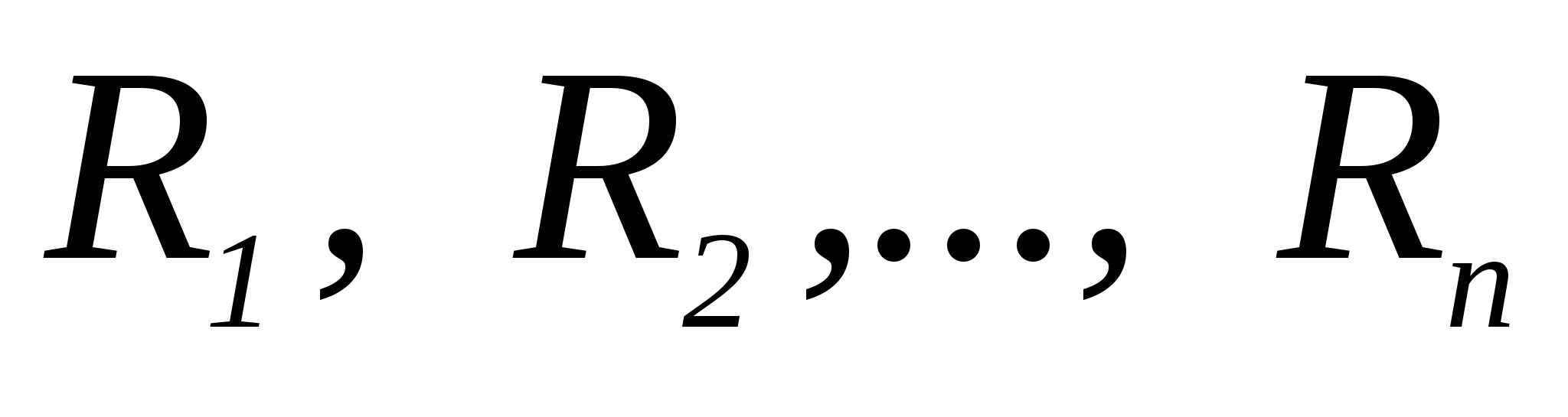 відношень між формулами, які називають правилами виведення.
відношень між формулами, які називають правилами виведення.
Для будь-якого ![]() є ціле додатне
є ціле додатне ![]() , таке, що для множини формул
, таке, що для множини формул ![]() і будь-якої формули
і будь-якої формули ![]() ефективно вирішується питання, чи знаходяться ці формули
ефективно вирішується питання, чи знаходяться ці формули ![]() у відношенні
у відношенні ![]() з формулою
з формулою ![]() , і якщо це так, то
, і якщо це так, то ![]() називають безпосереднім наслідком формул
називають безпосереднім наслідком формул ![]() за правилом
за правилом ![]() ├ А.
├ А.
Означення 2.1.2. Виведенням у теорії L називають таку послідовність формул ![]() , коли будь-яка з формул
, коли будь-яка з формул ![]() є або аксіомою, або безпосереднім наслідком деяких попередніх формул за одним із правил виведення.
є або аксіомою, або безпосереднім наслідком деяких попередніх формул за одним із правил виведення.
Означення 2.1.3. Теоремою теорії L називають таку формулу ![]() , коли існує виведення в теорії L формули
, коли існує виведення в теорії L формули ![]() , в якому останнім елементом є формула
, в якому останнім елементом є формула ![]() . Це виведення називають виведенням формули А в теорії L.
. Це виведення називають виведенням формули А в теорії L.
Якщо є алгоритм для перевірки, чи А є теоремою теорії L, то теорію L називають розв’язною теорією, інакше – теорією, що не є розв’язною.
Означення 2.1.4. Формулу А називають наслідком у теорії L множини формул Г тоді і тільки тоді, коли існує така послідовність формул ![]() , що
, що ![]() , і будь-яка з формул
, і будь-яка з формул ![]() є або аксіомою, або елементом Г, або безпосереднім наслідком деяких попередніх формул за одним із правил виведення.
є або аксіомою, або елементом Г, або безпосереднім наслідком деяких попередніх формул за одним із правил виведення.
Послідовність ![]() називають виведенням А із Г, а елементи множини Г – гіпотезами виведення.
називають виведенням А із Г, а елементи множини Г – гіпотезами виведення.
Запис ![]() ├ А означає, що А є наслідком множини формул Г. Якщо формула Г скінченна
├ А означає, що А є наслідком множини формул Г. Якщо формула Г скінченна ![]() ├ А, то пишуть
├ А, то пишуть ![]() ├ А. Якщо Г – порожня множина
├ А. Якщо Г – порожня множина ![]() , то запис
, то запис ![]() ├ А має місце тоді і тільки тоді, коли А є теорема. Замість
├ А має місце тоді і тільки тоді, коли А є теорема. Замість ![]() ├ А прийнято писати ├ А. Таким чином, ├ А є скороченим підтвердженням, що А – теорема.
├ А прийнято писати ├ А. Таким чином, ├ А є скороченим підтвердженням, що А – теорема.
Наведемо декілька простих властивостей поняття виведення із посилок.
-
Якщо
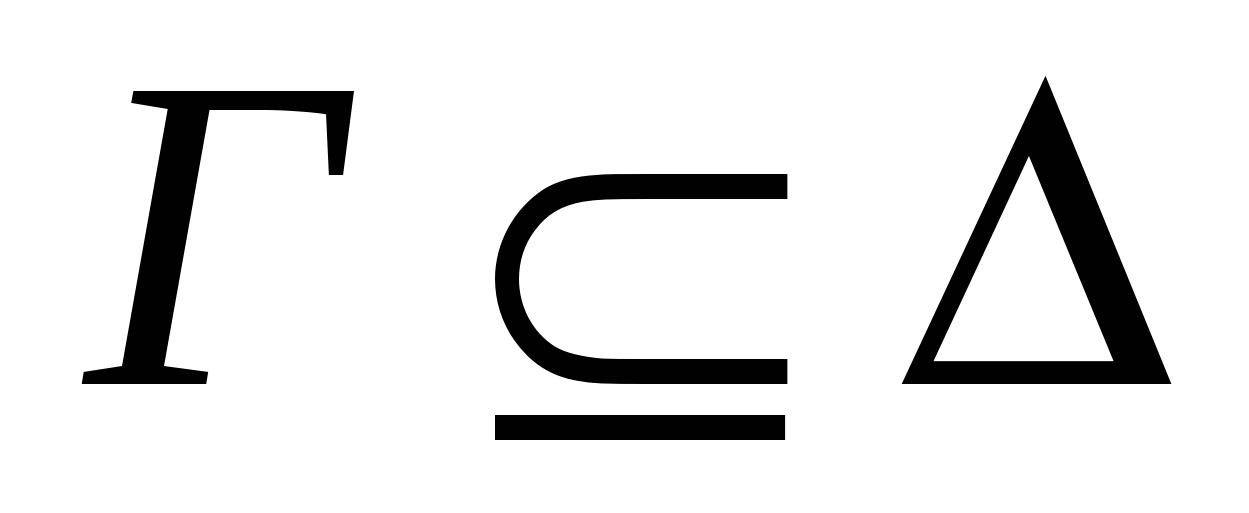 і
і 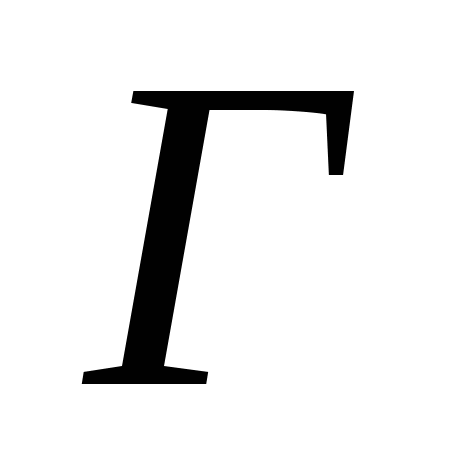 ├ А, то
├ А, то  ├ А.
├ А. -
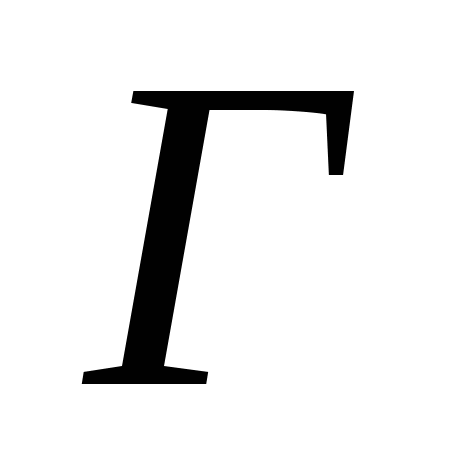 ├ А тоді і тільки тоді, коли в Г є скінченна підмножина
├ А тоді і тільки тоді, коли в Г є скінченна підмножина  , для якої
, для якої  ├ А.
├ А. -
Якщо
 ├ А і
├ А і 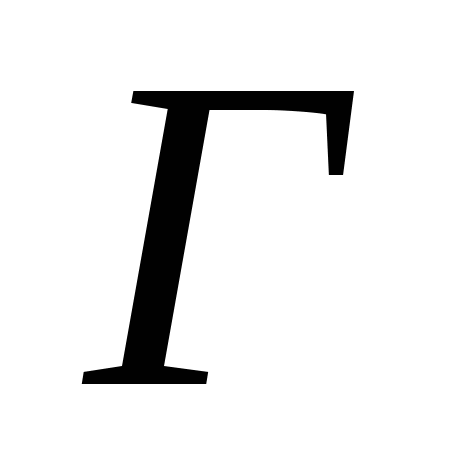 ├ А для будь-якого В із множини
├ А для будь-якого В із множини  , то
, то 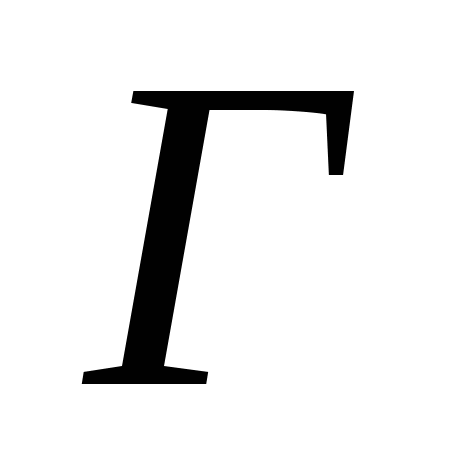 ├ А.
├ А.
Властивість 1 показує, що якщо А виведене із множини посилок Г, то вона залишиться виведеною, якщо додати до Г нові посилки. Частина “тоді” твердження 2 випливає із 1. Частина “тільки тоді” - це твердження є очевидним, якщо будь-яке виведення А із Г використовує скінченне число посилок із Г. Твердження 3 означає, якщо А вивідне із ![]() і кожна формула, яка є в
і кожна формула, яка є в ![]() , також вивідна з Г, то А виводимо із Г.
, також вивідна з Г, то А виводимо із Г.
Формальна аксіоматична теорія L для числення висловлювань задається таким способом.
- 1. Символами теорії L є
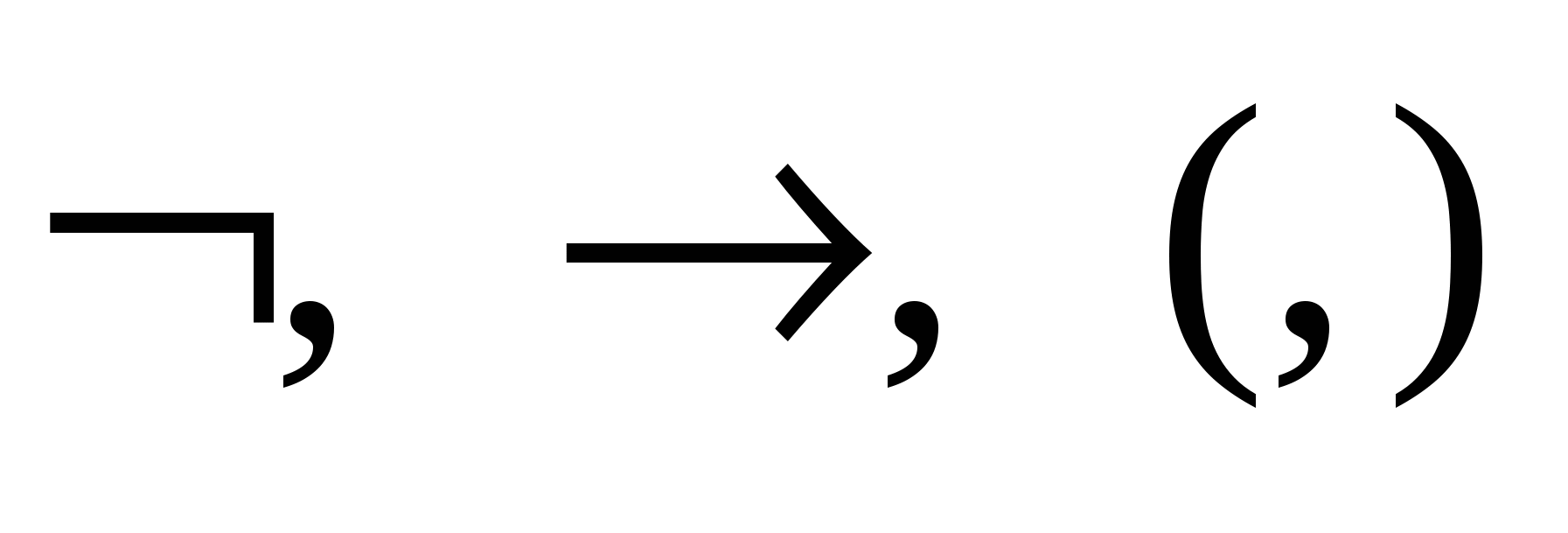 і букви Аі з цілими додатними числами якості індекси:
і букви Аі з цілими додатними числами якості індекси: 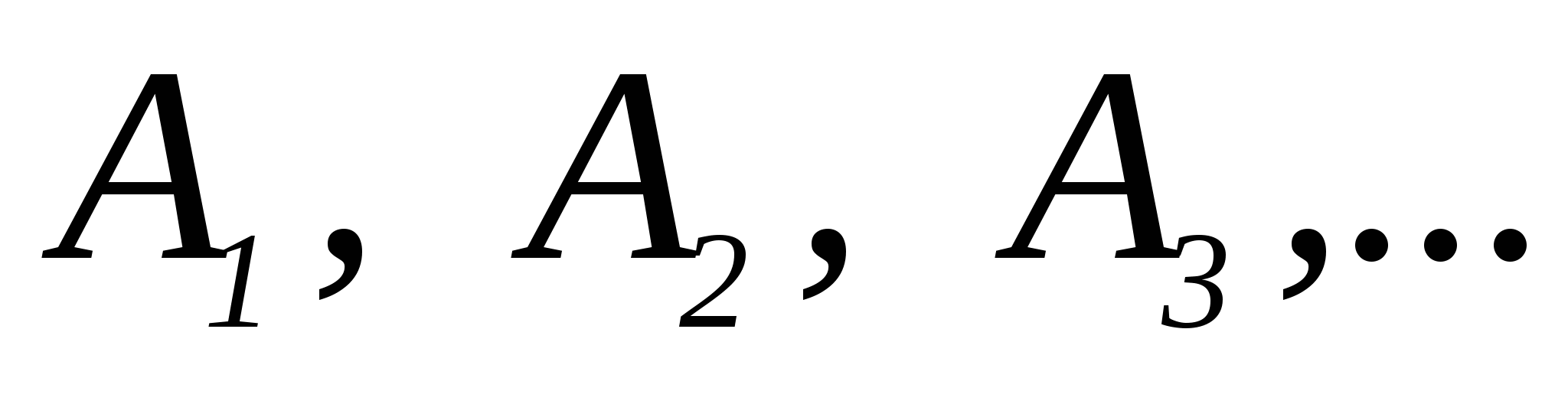 . Символи
. Символи 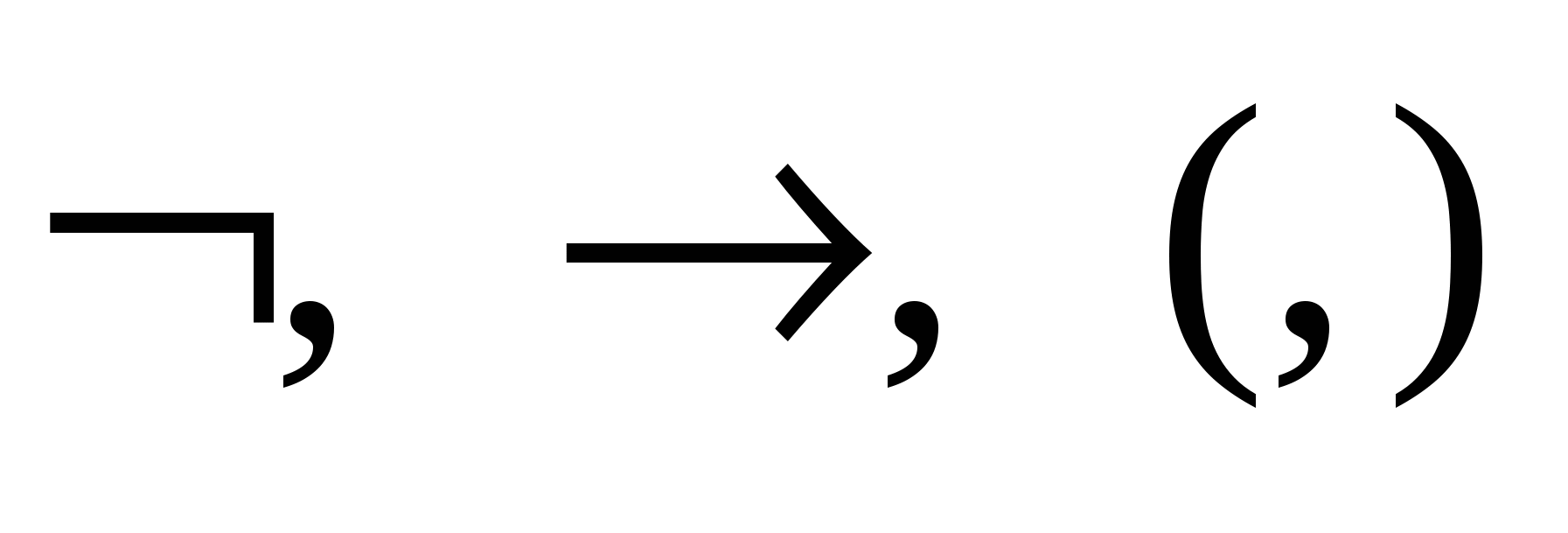 називають примітивними зв’язками, а Аі – пропозиційними змінними, або пропозиційними буквами.
називають примітивними зв’язками, а Аі – пропозиційними змінними, або пропозиційними буквами. - 2. Усі пропозиційні букви Аі є формулами. Якщо А і В - формули, то
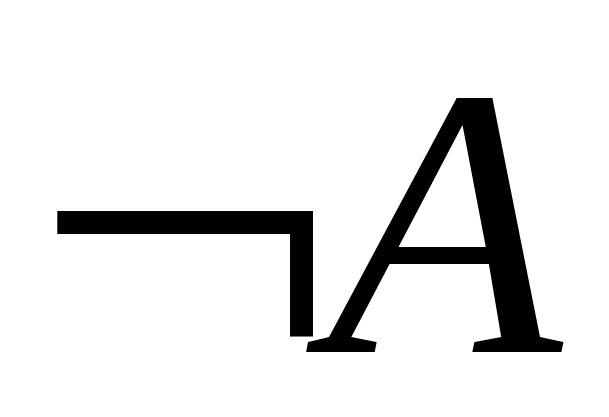 ,
,  теж формули теорії L.
теж формули теорії L. - 3. Для будь-яких формул А, В, С теорії L формули:
А1) ![]() ;
;
А2) ![]() ;
;
А3) ![]()
є аксіомами теорії L.
4. Єдиним правилом виведення служить правило modus ponens (MP), за допомогою якого із формули А і ![]() виводиться В :
виводиться В :
![]() ├ B.
├ B.
Необхідно зазначити, що нескінченна множина аксіом теорії L задана за допомогою тільки трьох схем аксіом А1, А2, А3, кожна з яких породжує нескінченну множину аксіом. Для будь-якою формули логіки висловлювань легко перевірити, є вона аксіомою чи ні, а звідси випливає, що теорія L є ефективно аксіоматизована теорія.
Інші зв’язки в аксіоматичній теорії L можна ввести за допомогою вже відомих формул
![]() ;
; ![]() ;
; ![]()
Теорема 2.1.1. Довести, що для будь-якої формули А виконується умова
├![]() . Знак ├
. Знак ├![]() - означає, що мова йде про теорію L.
- означає, що мова йде про теорію L.
Доведення. Побудову виведення формули ![]() виконаємо в теорії L.
виконаємо в теорії L.
-
Підставимо формулу
 у схему аксіоми А2, після чого отримаємо
у схему аксіоми А2, після чого отримаємо
![]()
-
Але формула
 - це є схема аксіоми А1.
- це є схема аксіоми А1. -
Використовуючи 1 і 2 за правилом MP, отримаємо
![]()
-
Використовуючи схему аксіоми А1, отримаємо
![]() .
.
-
Використовуючи 3 і 4 за правилом MP, отримаємо
![]() .
.
Необхідно зазначити, що кожна з аксіом А1,…,А3 є незалежна.
Існують інші аксіоматизації числення висловлювань, наприклад, Гільберта-Аккермана, Расселла, Кліні.
Логічними зв’язками аксіоматизації Гільберта-Аккермана є ![]() , а
, а ![]() служить скороченням для формули
служить скороченням для формули ![]() . Аксіоми є такими:
. Аксіоми є такими:
ГА1) ![]() ;
;
ГА2) ![]() ;
;
ГА3) ![]() ;
;
ГА4) ![]() .
.
Правилом виведення є МР.
Логічними зв’язками аксіоматизації Расселла є ![]() , а
, а ![]() ─ скорочення для формули
─ скорочення для формули ![]() . Його аксіоми мають такий вигляд:
. Його аксіоми мають такий вигляд:
РА1) ![]() ;
;
РА2) ![]() ;
;
РА3) ![]() .
.
Правилом виведення є МР.
Логічними зв’язками аксіоматизації Кліні є ![]() , аксіоми мають такий вигляд
, аксіоми мають такий вигляд
КА1) ![]() ;
;
КА2) ![]() ;
;
КА3) ![]() ;
;
КА4) ![]() ;
;
КА5) ![]() ;
;
КА6) ![]() ;
;
КА7) ![]() ;
;
КА8) ![]() ;
;
КА9) ![]() .
.
Правилом виведення є МР.
2.2. Теорема дедукції
Теорема дедукції дає нове правило виведення у логіці висловлювань, і тому вона є важливою при доведенні теорем і різних висловлювань.
Теорема дедукції 2.2.1. Якщо Г – множина формул, А і В – формули і Г, ![]() ├ В, то
├ В, то ![]() ├
├![]() . Зокрема, якщо
. Зокрема, якщо ![]() ├ В, то ├
├ В, то ├![]() .
.
Доведення. Нехай В1, В2,…, Вn – виведення із ![]() формули В, тобто Вn = В. Доведення будемо проводити індукцією по і – довжині виведення
формули В, тобто Вn = В. Доведення будемо проводити індукцією по і – довжині виведення ![]() формули В.
формули В.
При і=1 В1 повинно бути або а) елементом Г; б) аксіомою;
в) самою формулою А.
У випадках “а” і “б” теорема випливає з того, що за схемою А1 маємо ![]() . Звідси за МР отримаємо, що
. Звідси за МР отримаємо, що ![]() .
.
У випадку “б”, тобто коли ![]() , із доведеного вище маємо, що
, із доведеного вище маємо, що ![]() ├ А ─ теорема. Отже,
├ А ─ теорема. Отже, ![]() ├
├![]() і випадок і=1 цим вичерпано.
і випадок і=1 цим вичерпано.
Нехай тепер ![]() ├
├![]() справедливе для всіх
справедливе для всіх ![]() . Покажемо, що
. Покажемо, що ![]() ├
├![]() . У цьому випадку можливі такі варіанти
. У цьому випадку можливі такі варіанти
а) ![]() є аксіомою; б)
є аксіомою; б) ![]() є елементом Г;
є елементом Г;
в) ![]() ; г)
; г) ![]() є наслідком за правилом МР деяких формул
є наслідком за правилом МР деяких формул ![]() і
і ![]() , і
, і ![]() має вигляд
має вигляд ![]() .
.
Доведення випадків “а” - “в” нічим не відрізняється від доведення цих випадків для і=1.
У випадку “г”, використовуючи принцип індукції, маємо ![]() ├
├![]() і
і ![]() ├
├![]() .
.
За схемою аксіом А2 маємо ![]() Отже, за правилом МР отримаємо
Отже, за правилом МР отримаємо ![]() ├
├ ![]() і знову за правилом МР ─
і знову за правилом МР ─ ![]() , що й потрібно було довести.
, що й потрібно було довести.
Теорема 2.2.2. Довести, що ![]() ├
├![]() .
.
Доведення. За означенням теорії L
1) ![]() ─ гіпотеза;
─ гіпотеза;
2) ![]() ─ гіпотеза;
─ гіпотеза;
3) А ─ гіпотеза;
4) Використовуючи МР із 1 і 3, отримаємо В;
5) Використовуючи МР із 2 і 4, отримаємо С.
Отже, ![]() ├ С і за теоремою дедукції маємо
├ С і за теоремою дедукції маємо ![]() ├
├![]() що й потрібно було довести.
що й потрібно було довести.
Теорема 2.2.3. Довести, що ![]() В ├
В ├ ![]()
Доведення. За означенням теорії L
-
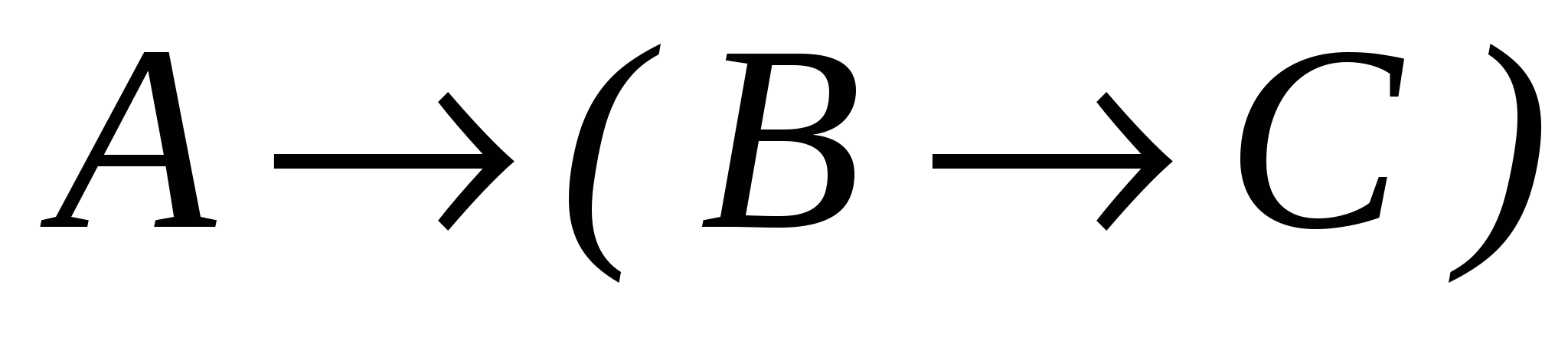 ─ гіпотеза;
─ гіпотеза; -
В ─ гіпотеза;
-
А ─ гіпотеза;
-
використовуючи МР із 1 і 3, отримаємо
 ;
; -
використовуючи МР із 2 і 4, отримаємо С.
Отже, ![]() ├ С, і за теоремою дедукції маємо
├ С, і за теоремою дедукції маємо ![]() В ├
В ├![]() , що і потрібно було довести.
, що і потрібно було довести.
Теорема 2.2.4. Для будь-яких формул А і В такі формули є теоремами формальної теорії L:
а) ![]() ; д)
; д) ![]() ;
;
б) ![]() ; є)
; є) ![]() ;
;
в) ![]() ; ж)
; ж) ![]() .
.
г) ![]() ;
;
а) ├![]()
Доведення
- 1.
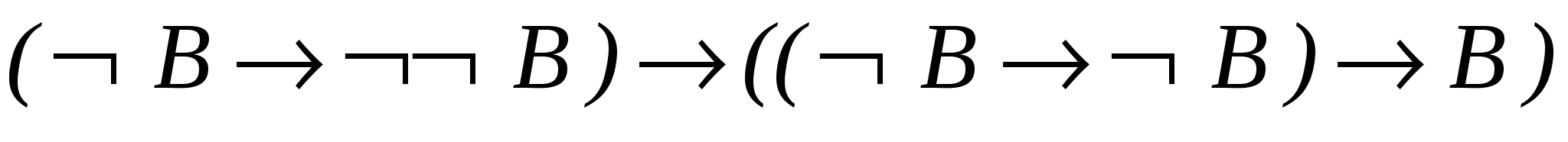 – схема аксіом А3;
– схема аксіом А3; - 2.
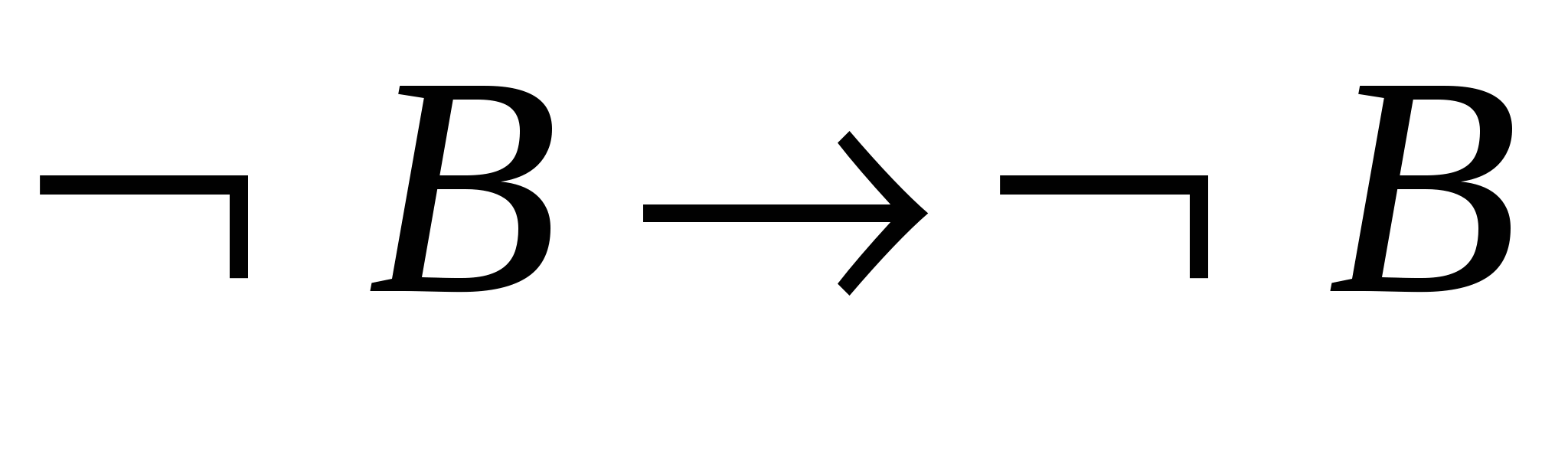 – теорема 2.1.1;
– теорема 2.1.1; - 3.
 – теорема 2.2.3;
– теорема 2.2.3; - 4.
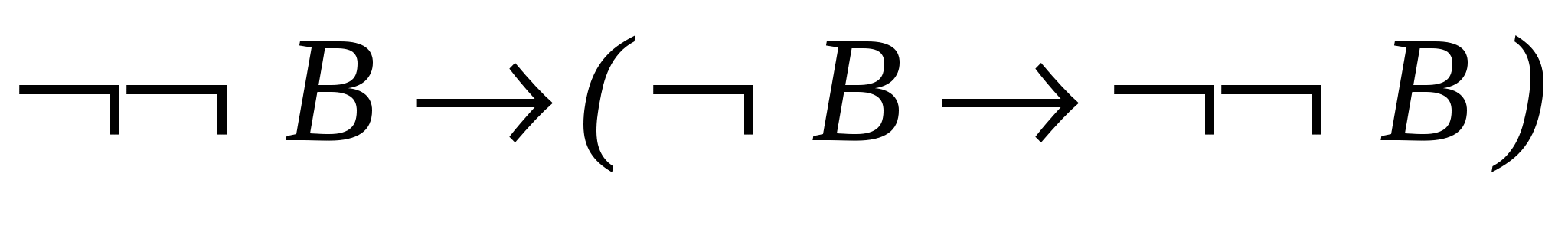 – схема аксіом А1;
– схема аксіом А1; - 5.
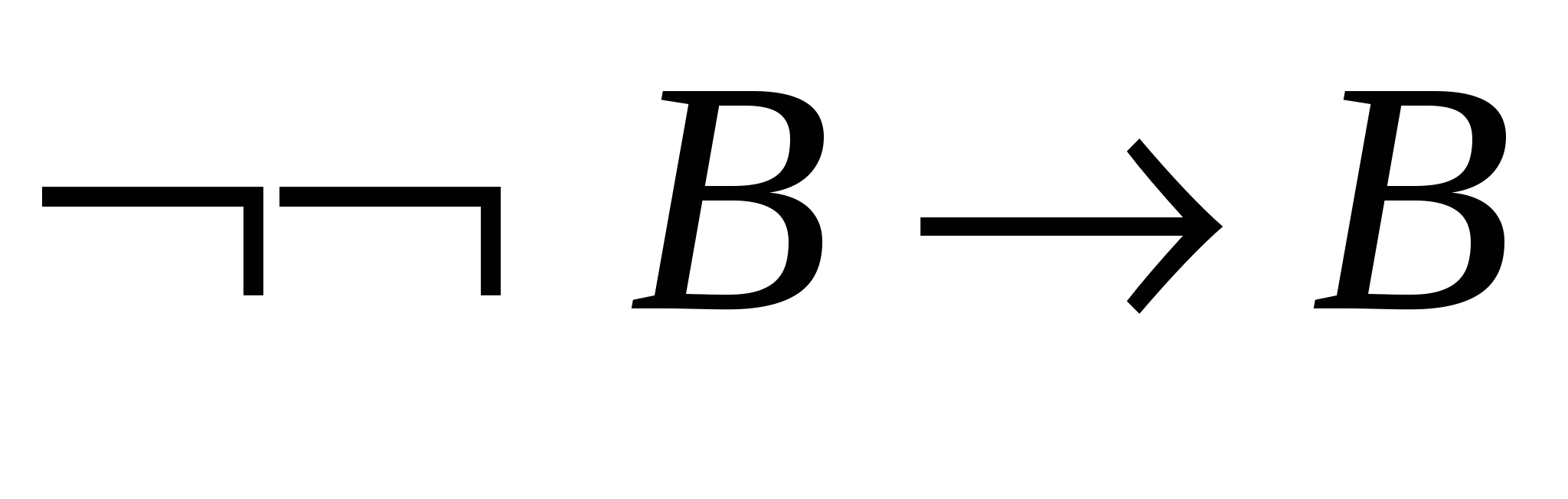 –
–
б)![]() .
.
Доведення
- 1.
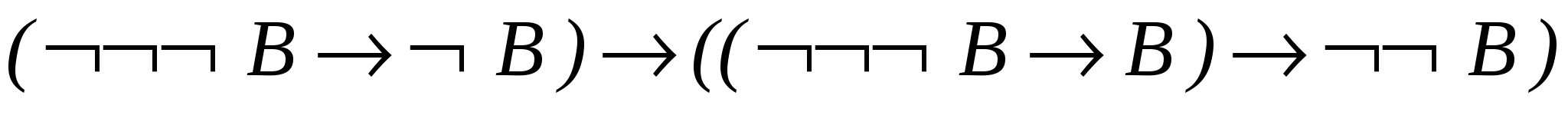 – схема аксіом А3;
– схема аксіом А3; - 2.
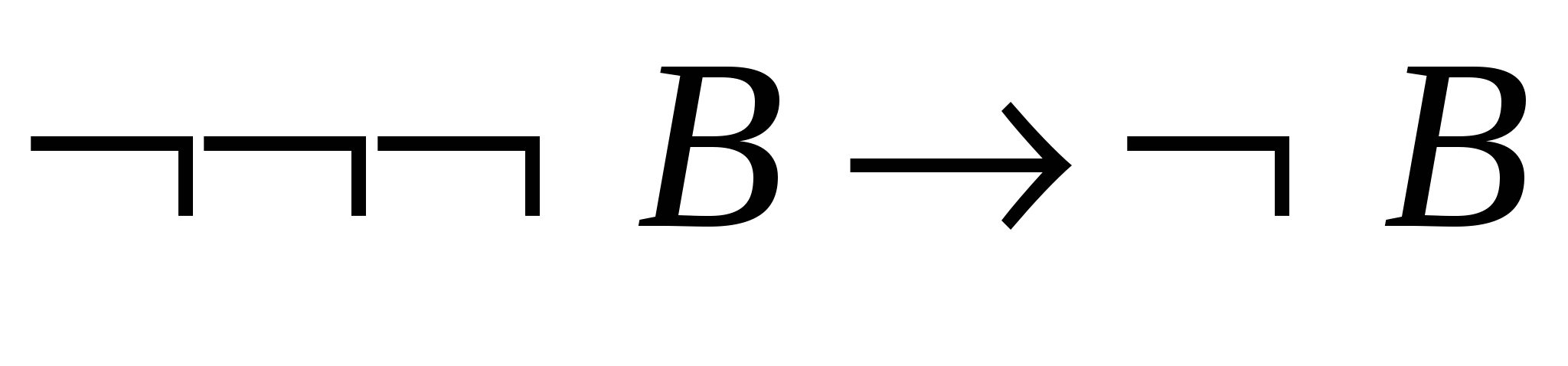 – теорема 2.2.4а;
– теорема 2.2.4а; - 3.
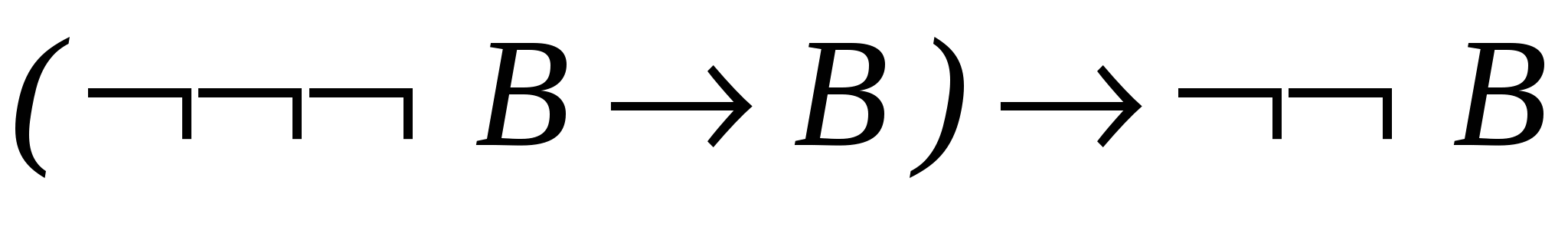 – за МР із 1 і 2;
– за МР із 1 і 2; - 4.
 – схема аксіом А1;
– схема аксіом А1; - 5.
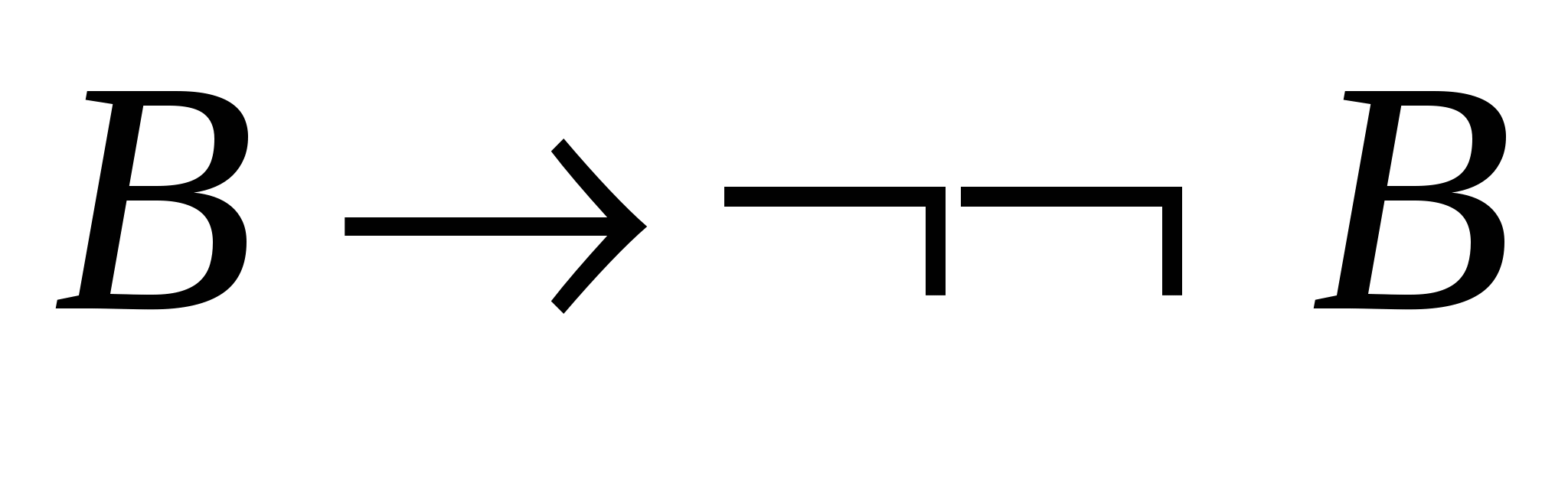 – теорема 2.2.2 і за МР із 3 і 4.
– теорема 2.2.2 і за МР із 3 і 4.
Зіставляючи теореми 2.2.4а і 2.2.4б, отримаємо теорему
![]() ,
,
яка виражає відомий нам із алгебри логіки закон подвійного заперечення.
в) ├![]()
Доведення
- 1.
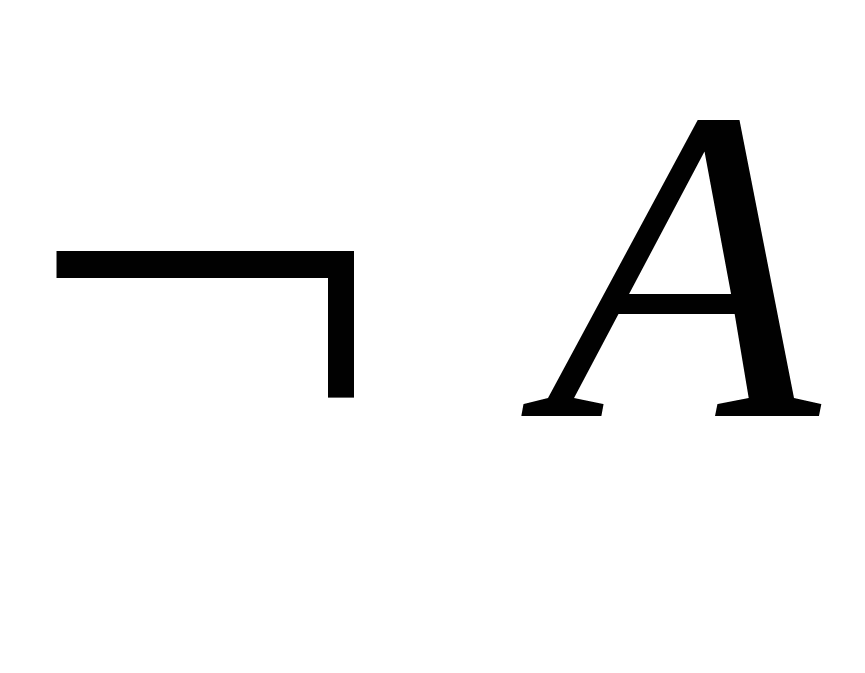 – гіпотеза;
– гіпотеза; - 2.
 – гіпотеза;
– гіпотеза; - 3.
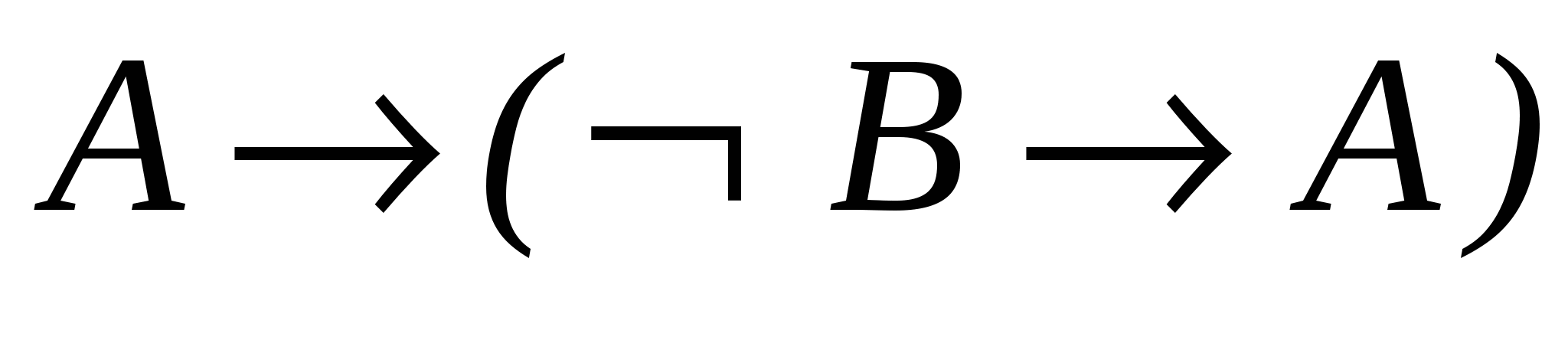 – схема аксіом А1;
– схема аксіом А1; - 4.
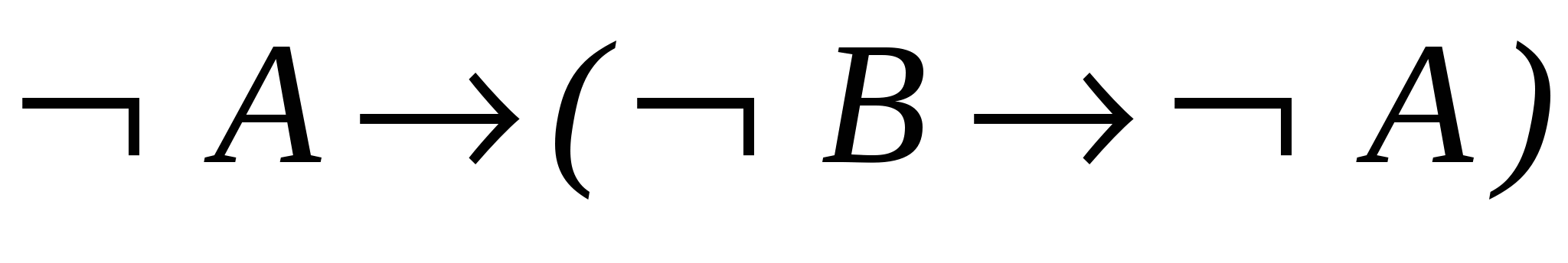 – схема аксіом А1;
– схема аксіом А1; - 5.
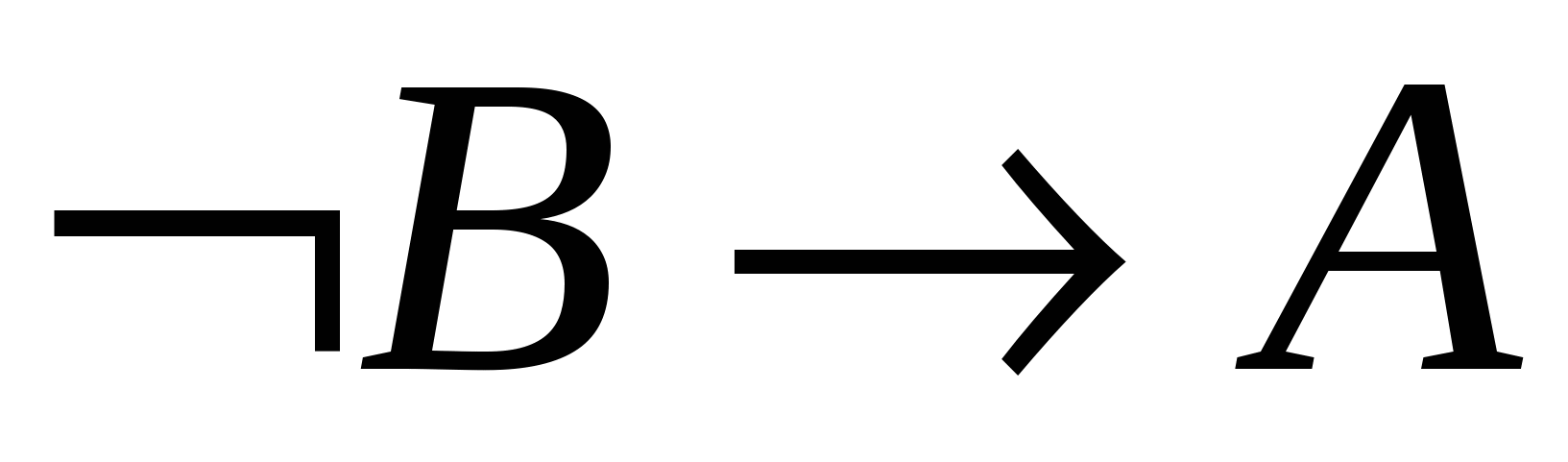 – за МР із 2, 3;
– за МР із 2, 3; - 6.
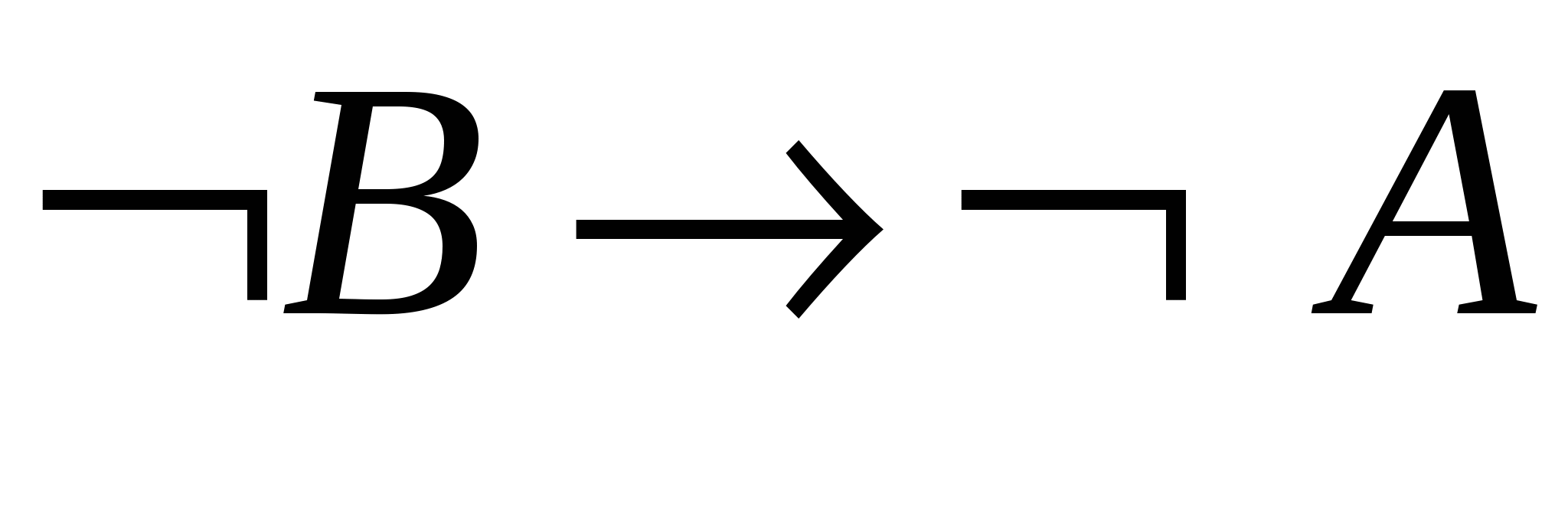 – за МР із 1, 4;
– за МР із 1, 4; - 7.
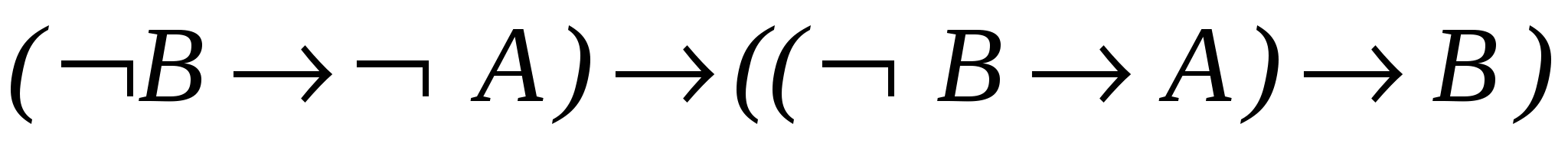 – схема аксіом А3;
– схема аксіом А3; - 8.
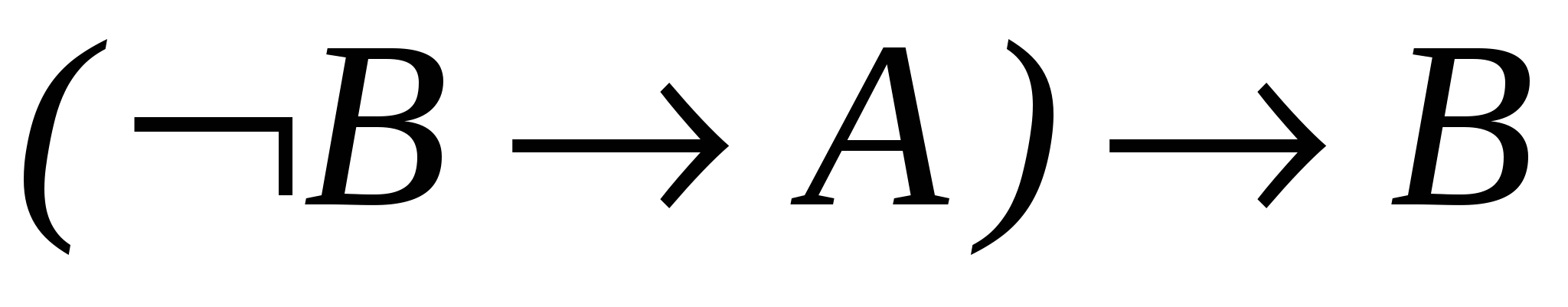 – за МР із 6, 7;
– за МР із 6, 7; - 9.
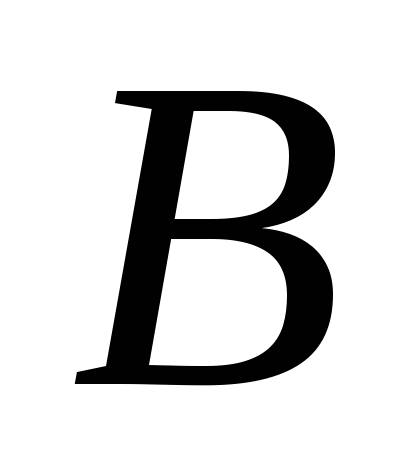 – за МР із 5, 8.
– за МР із 5, 8.
Отже, використовуючи 1 ─ 9, маємо, що ![]() ├ В і за теоремою дедукції отримаємо ├
├ В і за теоремою дедукції отримаємо ├![]() .
.
г) ├ ![]()
Доведення
- 1.
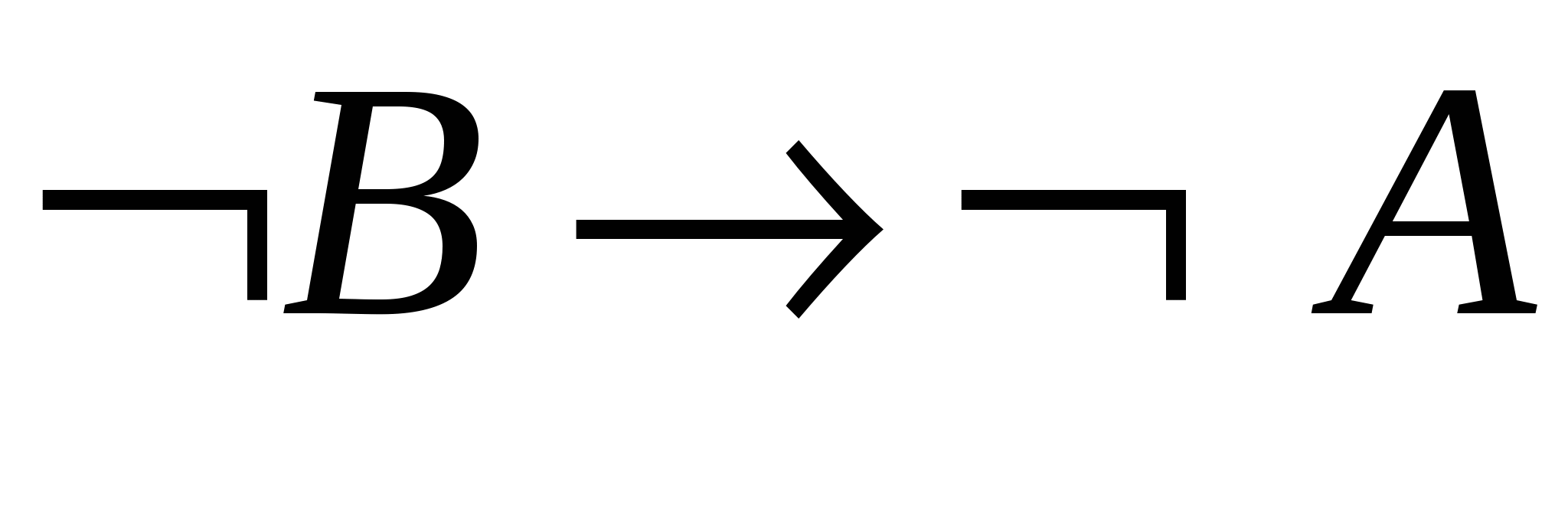 – гіпотеза;
– гіпотеза; - 2.
 – гіпотеза;
– гіпотеза; - 3.
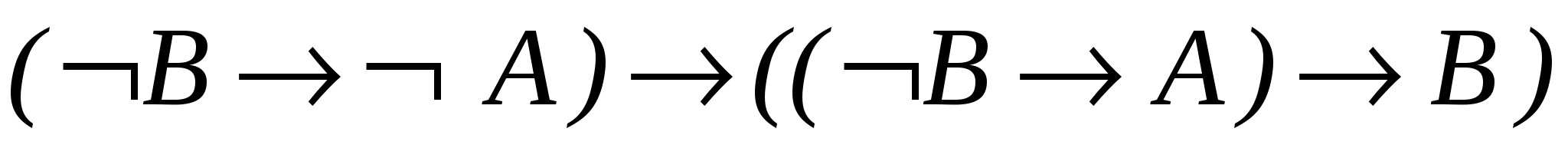 – схема аксіом А3;
– схема аксіом А3; - 4.
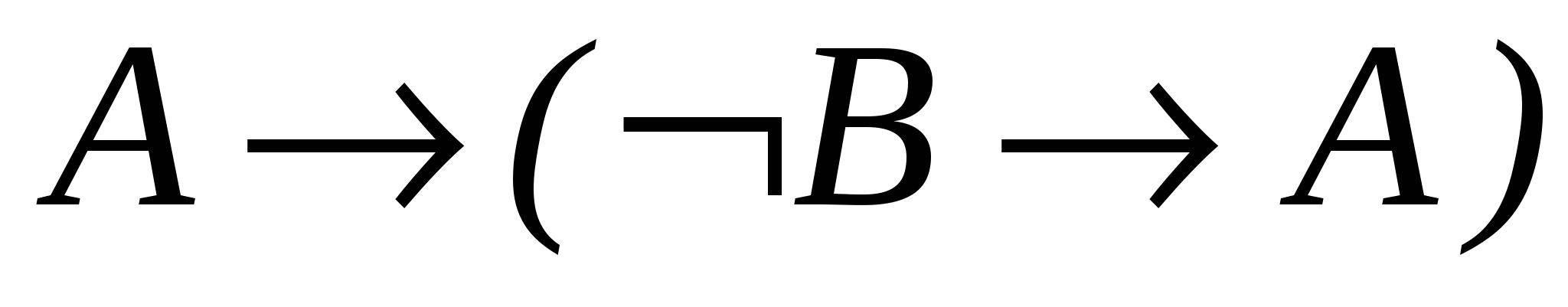 – схема аксіом А1;
– схема аксіом А1; - 5.
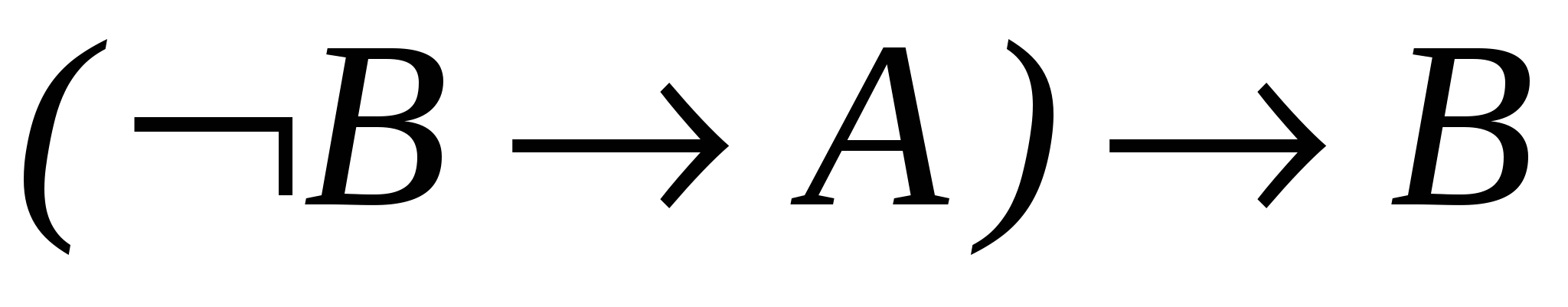 – за МР із 1, 3;
– за МР із 1, 3; - 6.
 – теорема 2.2.2;
– теорема 2.2.2; - 7.
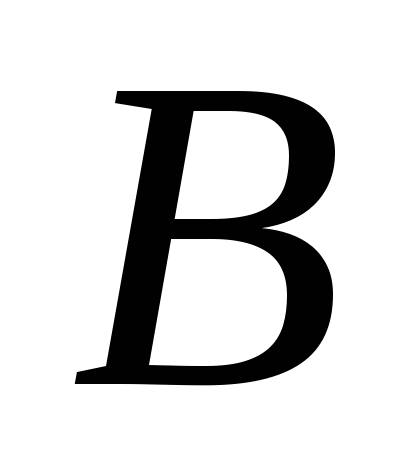 – за МР із 2, 6.
– за МР із 2, 6.
Отже, використовуючи 1─7 маємо, що ![]() ├ В і, двічі застосувавши дедукції, отримаємо ├
├ В і, двічі застосувавши дедукції, отримаємо ├ ![]()
д) ![]() .
.
Доведення
- 1.
 – гіпотеза;
– гіпотеза; - 2.
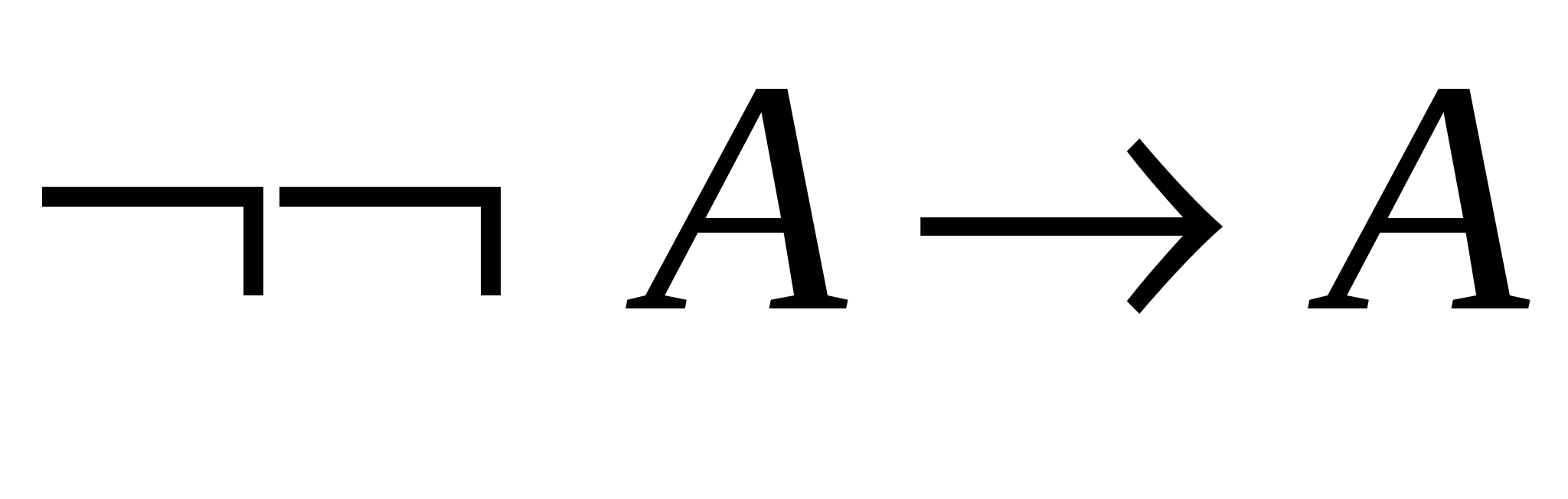 – теорема 2.2.4а;
– теорема 2.2.4а; - 3.
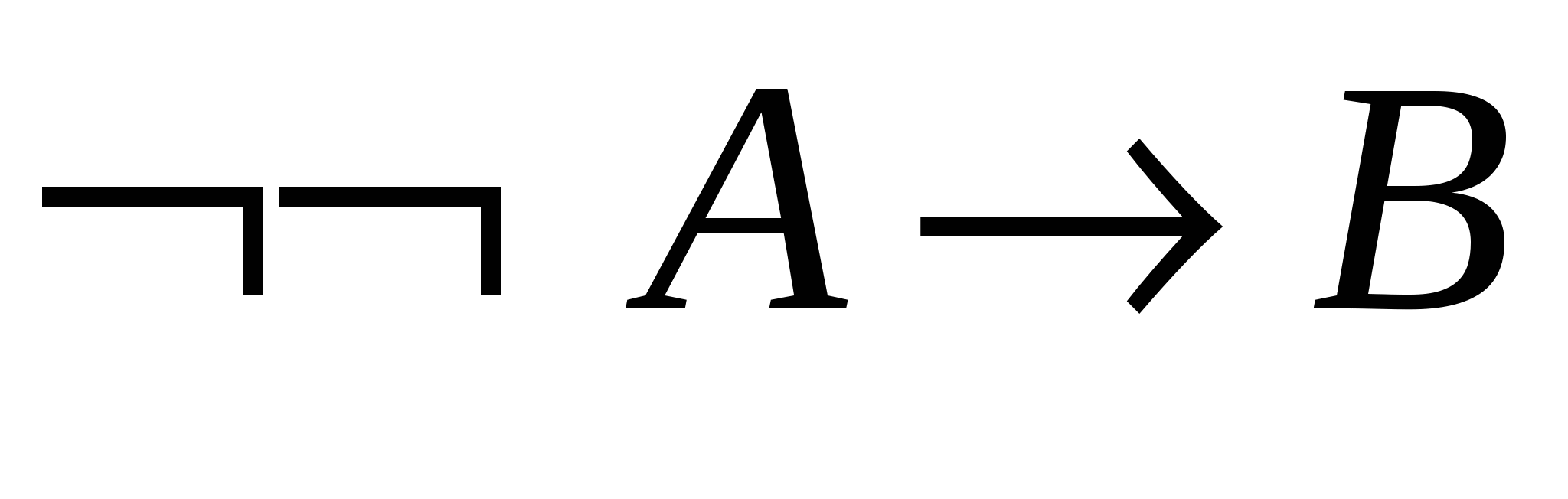 – теорема 2.2.2;
– теорема 2.2.2; - 4.
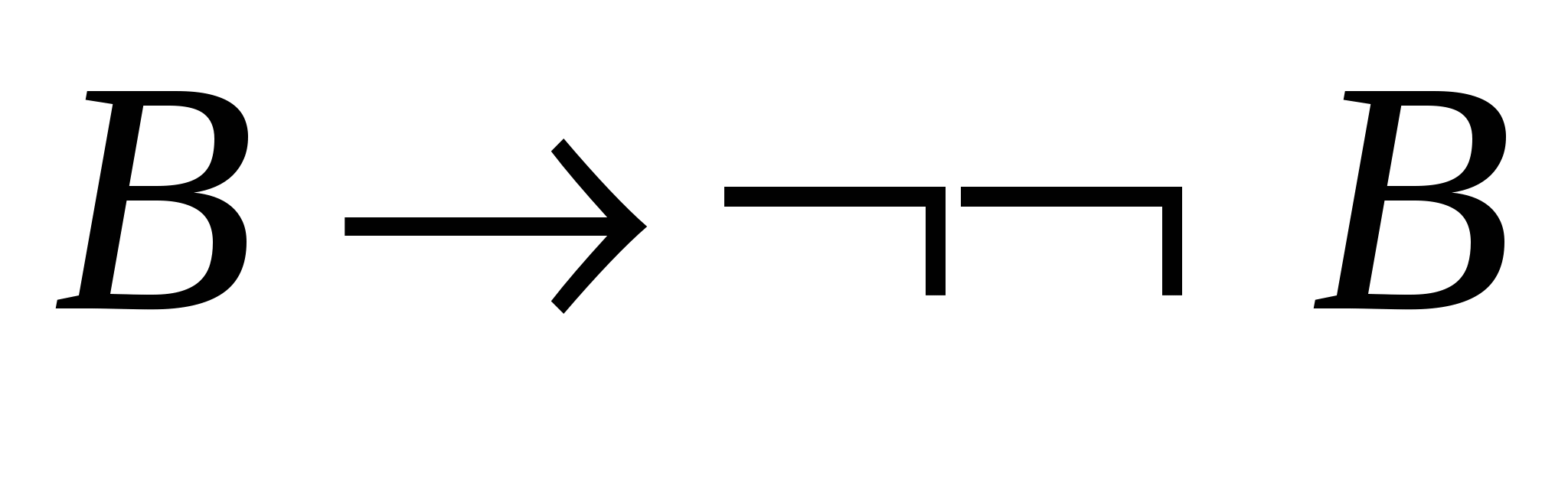 – теорема 2.2.4б;
– теорема 2.2.4б; - 5.
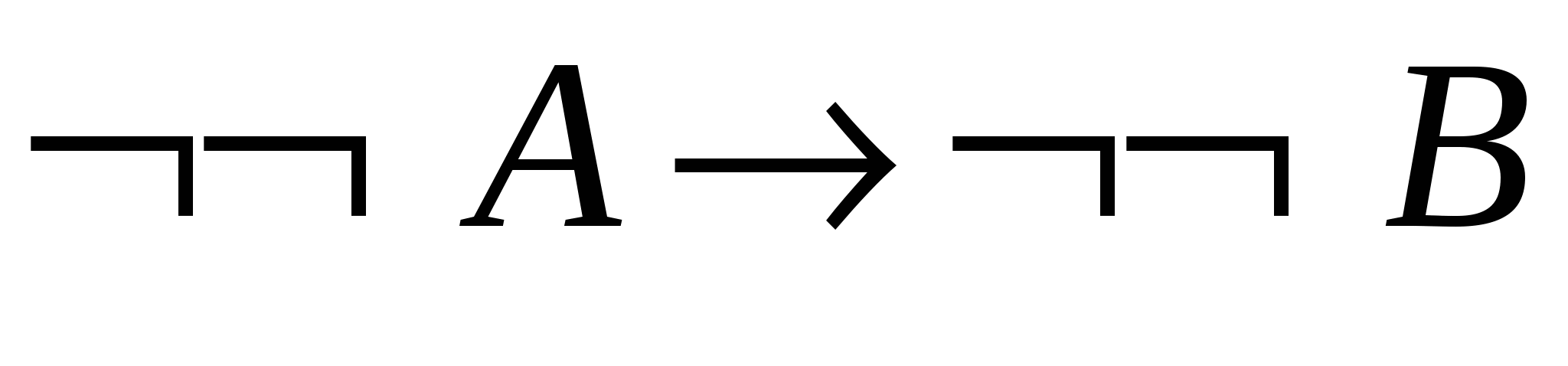 – теорема 2.2.2;
– теорема 2.2.2; - 6.
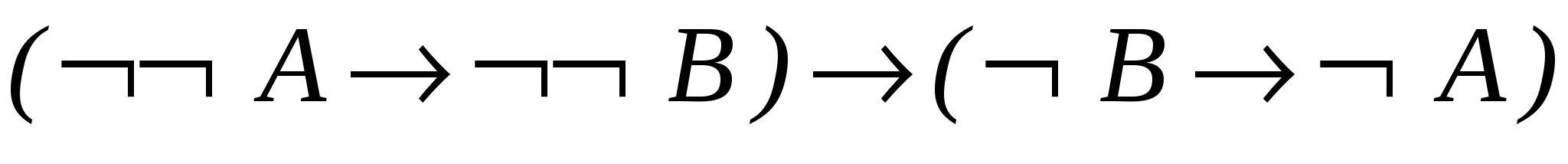 – теорема 2.2.4д;
– теорема 2.2.4д; - 7.
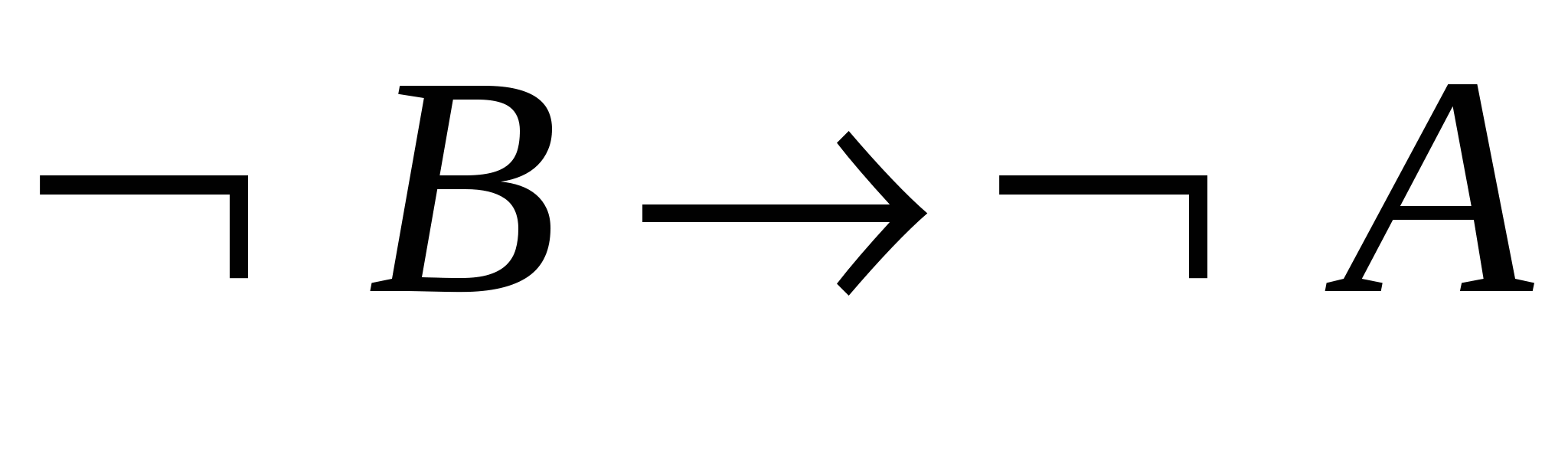 – за МР із 5, 6.
– за МР із 5, 6.
Отже, використовуючи 1─7 маємо ![]() ├
├ ![]() і за теоремою отримаємо ├
і за теоремою отримаємо ├ ![]()
Порівнюючи теореми 2.2.1г і 2.2.1д, отримаємо теорему
![]()
на якій ґрунтується метод доведення тверджень, відомий під назвою метод доведення від супротивного.
е) ├![]()
Доведення. Оскільки А, ![]() ├ В, то за теоремою отримаємо
├ В, то за теоремою отримаємо ![]()
За теоремою 2.2.4д маємо
├ ![]()
Використовуючи теорему 2.2.2, отримаємо
├ ![]()
є) ![]()
Доведення.
- 1.
 – гіпотеза.
– гіпотеза. - 2.
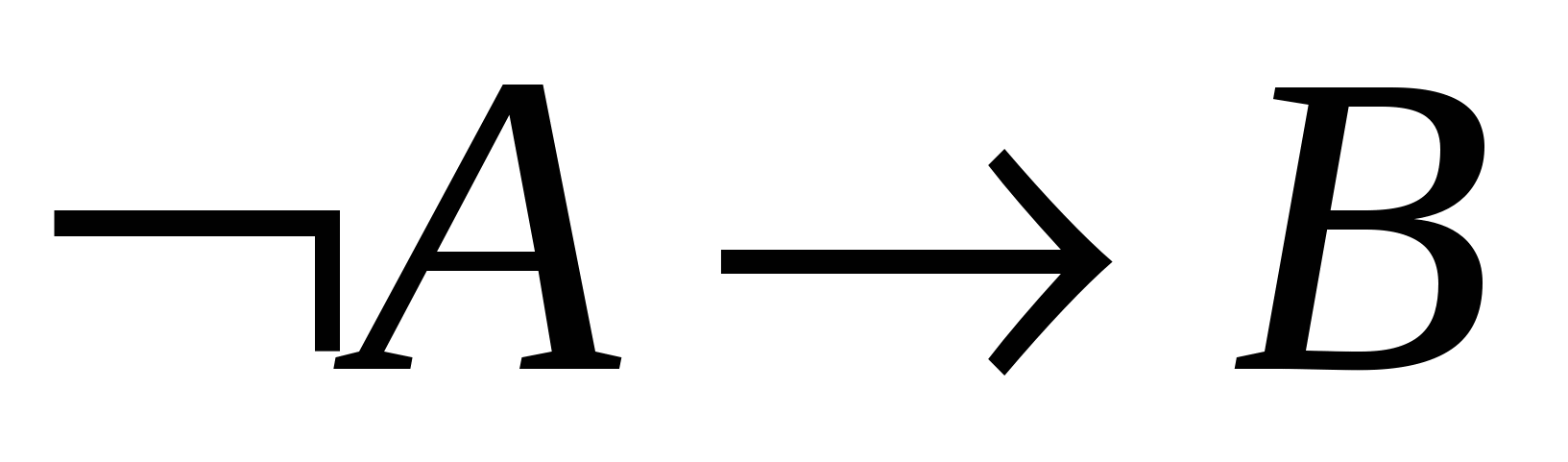 ─ гіпотеза.
─ гіпотеза. - 3.
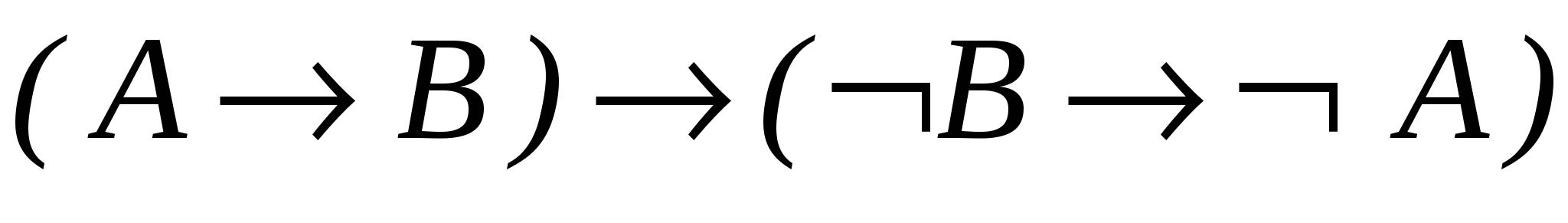 ─ теорема 2.2.4 д.
─ теорема 2.2.4 д. - 4.
 ─ за МР із 1,3.
─ за МР із 1,3. - 5.
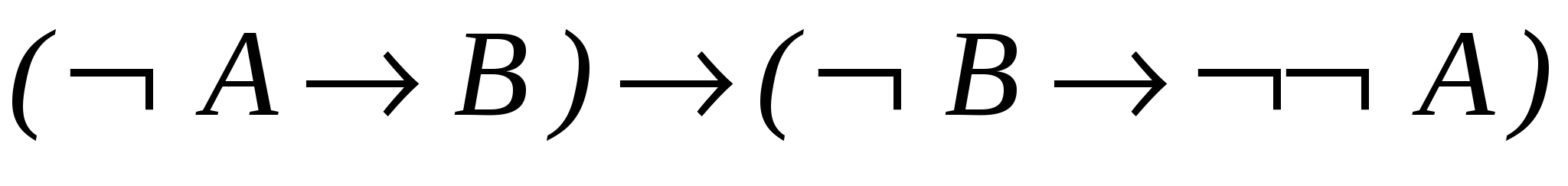 ─ теорема 2.2.4.д..
─ теорема 2.2.4.д.. - 6.
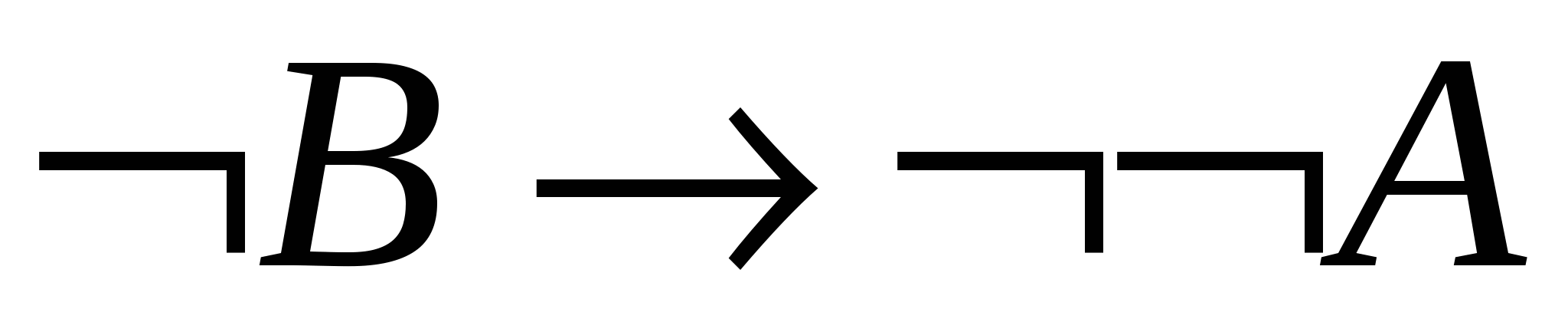 ─ за МР із 2,5;
─ за МР із 2,5; - 7.
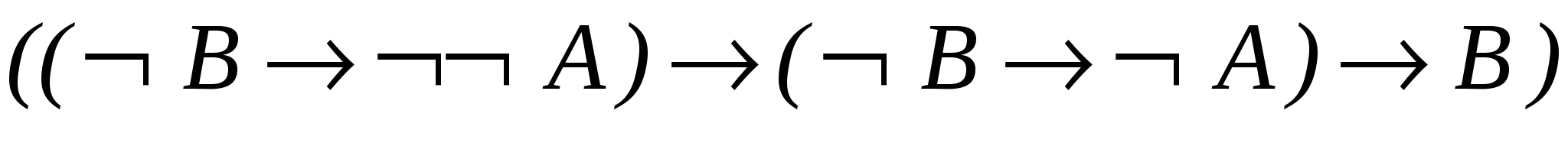 ─ схема аксіом АЗ.
─ схема аксіом АЗ.
- 8.
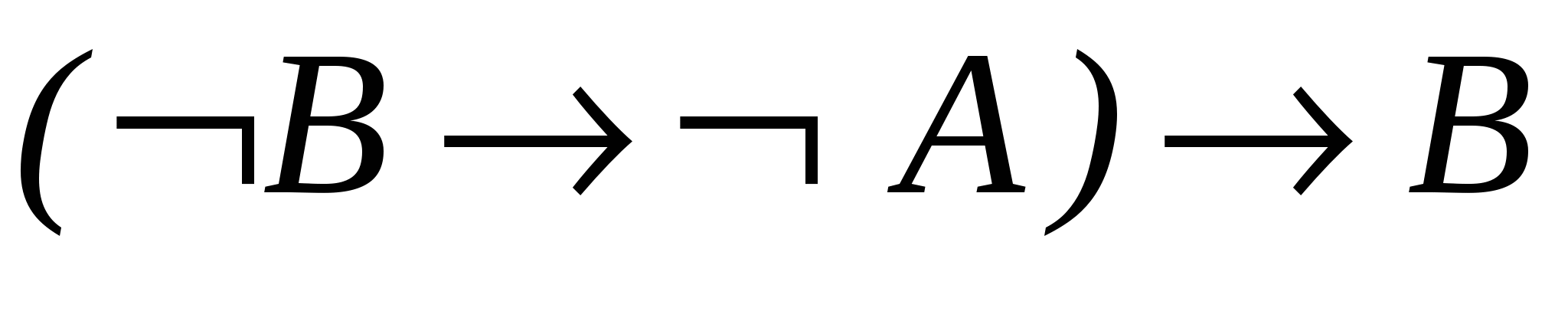 ─ за МР із 6,7.
─ за МР із 6,7. - 9.
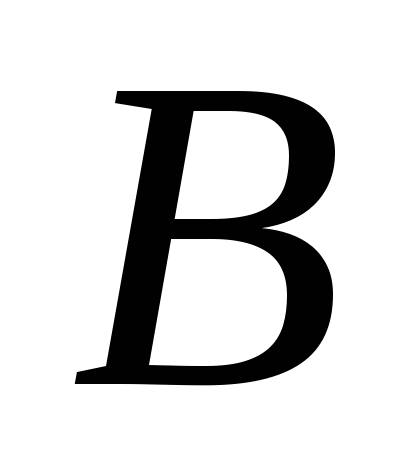 ─ за МР із 4,8.
─ за МР із 4,8.
Отже, ![]() ,
, ![]() ├
├![]() , і застосувавши двічі теорему дедукції, отримаємо
, і застосувавши двічі теорему дедукції, отримаємо
├![]() .
.
2.3. Побудова доведень у логіці висловлювань
Логіка ─ це наука про способи доведення. У звичайній логіці всі доведення будуються на відношенні еквівалентності, а в логіці висловлювань – на відношенні порядку, тобто на відношенні, яке є між причиною і наслідком. При цьому дуже важливо в логіці висловлювань відрізняти мови і мета мови, об’єктні та суб’єктні висловлювання. При нехтуванні цією різницею є ризик потрапити в протиріччя, яке називають логічним парадоксом. Розглянемо дію такого парадоксу на практиці: “Парадокс брехуна”. “Я брехун”, – сказав брехун. Але оскільки брехун каже про себе, що він брехун, то він виступає у своїй протилежній якості, а саме небрехуна. Тому наведене висловлювання необхідно розуміти інакше “Я брехун”, – сказав небрехун. Але тепер із цього висловлювання випливає, що правдивий чоловік повідомляє про себе, що він брехун. Правдивому чоловікові потрібно вірити. Тому друге висловлювання необхідно розуміти все-таки так, я все це відтворено в першому висловлюванні. Таким чином, виникає невизначеність, яка полягає в тому, що незрозуміло, як кваліфікувати того, хто говорить, – як брехуна чи як не брехуна, а звідси ідентифікувати як істинне чи як хибне.
Логічний парадокс тут виник тому, що в наведених висловлюваннях не робиться розділення між двома принципово різними логічними рівнями. Тут, крім “брехуна” чи “небрехуна”, у цій логічній ситуації бере участь суб’єкт “метаспостерігач”. Якщо провести чітке синтаксичне відділення смислового змісту, яке повинно стосуватися до нас як метаспостерігачів, від іншої семантики об’єктних персонажів, то логічну суперечність буде знято. Тоді ситуацію з брехуном можна подати таким чином.
“Я брехун”, – сказав брехун.
“Це істина”, – сказав метаспостерігач.
“Я брехун”, – сказав небрехун.
“Це хибно”, – сказав метаспостерігач.
“Я небрехун”, – сказав брехун.
“Це хибно”, – сказав метаспостерігач.
“Я небрехун”, – сказав небрехун.
“Це істина”, – сказав метаспостерігач.
Для розпізнавання мови логіки висловлювань і метамови дослідника між посилками і наслідком замість об’єктивного символу імплікації “![]() ” будемо ставити суб’єктивний символ метаімплікації “
” будемо ставити суб’єктивний символ метаімплікації “![]() ”, а між посилками замість об’єктивних символів кон’юнкції “
”, а між посилками замість об’єктивних символів кон’юнкції “![]() ” і диз’юнкції “
” і диз’юнкції “![]() ”, ставити суб’єктивні символи метакон’юнкції “
”, ставити суб’єктивні символи метакон’юнкції “![]() ” і метадиз’юнкції “
” і метадиз’юнкції “![]() ”.
”.
Тоді твердження, яке необхідно довести, в логіці висловлювань можна оформити у вигляді такого причинно-наслідкового відношення:
![]() , (2.3.1)
, (2.3.1)
де ![]() – посилка (причина);
– посилка (причина); ![]() – висновок (наслідок).
– висновок (наслідок).
Читається: “Якщо посилки ![]() істинні, то і висновок
істинні, то і висновок ![]() також істинний”, або “Якщо причини
також істинний”, або “Якщо причини ![]() мали місце, то матиме місце і наслідок”.
мали місце, то матиме місце і наслідок”.
Щоб не переплутати об’єктивне висловлювання із суб’єктивним висловлюванням, справедливість якого необхідно встановити, домовимося речення 2.3.1. називати клаузою (clause).
Означення 2.3.1. Клаузою називають метапропозицію, в якій виконується відношення порядку, оформлене через символ метаімплікації “![]() ”.
”.
Як і відношення еквівалентності, відношення порядку задовольняє три закони:
-
рефлективності –
 ;
; -
антисиметричності – якщо
 , то
, то 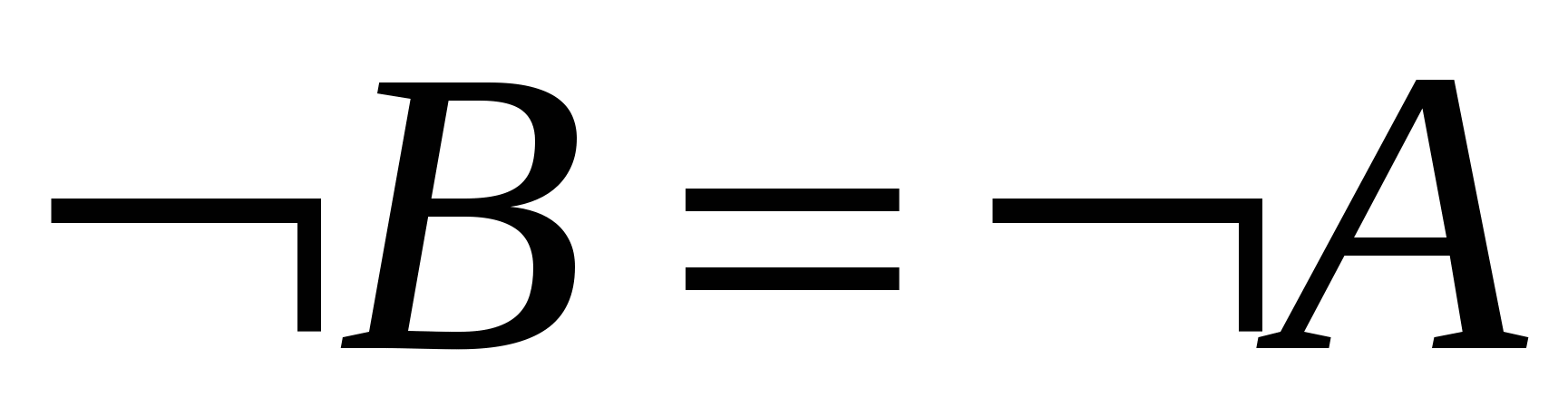 ;
; -
транзитивності – якщо
 і
і  , то
, то 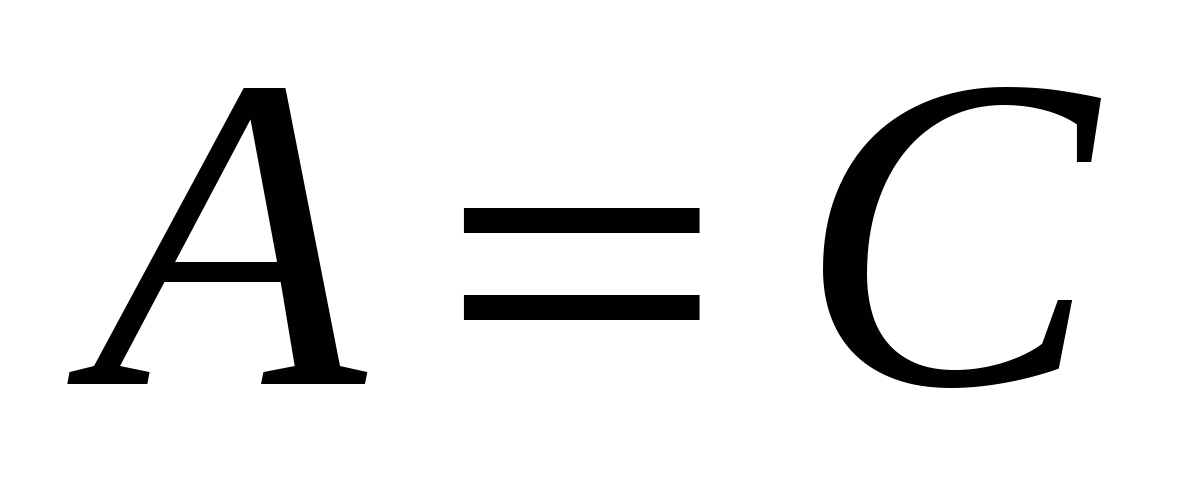 .
.
На відміну від еквівалентності відношення порядку припускає виконання закону антисиметричності, який можна записати так:
якщо ![]() і
і ![]() , то
, то ![]() .
.
Замість букв у клаузі можна підставляти об’єктивні висловлювання, і тоді вона наповнюється конкретним змістом, який іменується семантикою, або легендою. Наприклад, нехай задана клауза
![]() ,
, ![]() .
.
Якщо прийняти, що ![]() “блиснула блискавка”, а
“блиснула блискавка”, а ![]() “грянув грім”, то можна скласти таку легенду: “Відомо, що якщо блиснула блискавка, то після цього гряне грім. Блиснула блискавка. Тому повинен грянути грім”.
“грянув грім”, то можна скласти таку легенду: “Відомо, що якщо блиснула блискавка, то після цього гряне грім. Блиснула блискавка. Тому повинен грянути грім”.
Над суб’єктом, який формулює метапропозиції, може стояти другий суб’єкт, для якого уже пропозиції першого суб’єкта будуть об’єктивні. Тоді клаузу 2.3.1 другий суб’єкт, або метасуб’єкт, запише для себе таким логічним виразом: ![]() .
.
Перетворивши цей вираз у диз’юнкцію, отримаємо
![]() .
.
Звідси знаходимо:
![]() . (2.3.2)
. (2.3.2)
Клауза 2.3.2. може бути подана в другій еквівалентній формі
![]() (2.3.3)
(2.3.3)
Унаслідок комутативності кон’юнкції на місці посилки ![]() може бути будь-яка посилка і причому не одна. Наприклад, клауза
може бути будь-яка посилка і причому не одна. Наприклад, клауза
![]() .
.
може бути перетворена в іншу еквівалентну форму:
![]() (2.3.4)
(2.3.4)
Однак клауза 2.3.1 порівняно з 2.3.3 й іншими подібними формами типу 2.3.4 має певні переваги, які дають можливість використати її в мові логічного програмування ПРОЛОГ. Її називають хорнівською. Задовільну клаузу завжди можна звести шляхом еквівалентних перетворень до хорнівського вигляду.
Якщо символ метаімплікації “![]() ” клаузи 2.3.1 перемістити в крайнє ліве положення, то вона перетвориться в тавтологію, а якщо в крайнє праве положення, то в суперечність:
” клаузи 2.3.1 перемістити в крайнє ліве положення, то вона перетвориться в тавтологію, а якщо в крайнє праве положення, то в суперечність: ![]() – тавтологія,
– тавтологія, ![]() – протиріччя.
– протиріччя.
2.4. Аксіоматичний метод
Аксіоматичний метод перевірки тотожної істинності логічних висловлювань ґрунтується на тому, щоб серед нескінченного числа істинних
клауз знайти незалежну систему аксіом, за допомогою якої можна було
установити справедливість будь-яких клауз.
Оскільки доведення в логіці висловлювань будуються на відношенні порядку, то логіка висловлювань є розширенням логіки Буля. Тому всі істинні тотожності логіки Буля автоматично стають справедливими клаузами логіки висловлювань. Наприклад, закон склеювання логіки Буля ![]() можна подати такими клаузами:
можна подати такими клаузами:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ~
~![]() ,
, ![]() .
.
Таким чином, незалежна система аксіом логіки Буля, яка складається з чотирьох законів – комутативності, асоціативності, дистрибутивності, нуля і одиниці, – автоматично стає системою аксіом і логіки висловлювань. Для визначення відношення порядку необхідне будь-яке одне елементарне висловлювання, до якого можна було зводити всі інші найбільш складні висловлювання. Таким висловлюванням може бути очевидна думка: “Істину може висловлювати кожний”.
Використовуючи формальну мову логіки висловлювань, цю думку можна подати такою кляузою: ![]() , яка означає “якщо
, яка означає “якщо ![]() істинне, то джерелом цієї істинності може бути що завгодно, наприклад
істинне, то джерелом цієї істинності може бути що завгодно, наприклад ![]() ”. Якщо зробити еквівалентне перетворення, то отримаємо клаузу
”. Якщо зробити еквівалентне перетворення, то отримаємо клаузу
![]() . (2.4.1)
. (2.4.1)
Семантика цієї клаузи теж змінилася, і матиме таке висловлювання: “якщо раніше було встановлено, що ![]() істинне, то істинність
істинне, то істинність ![]() не може проявитися так, щоб
не може проявитися так, щоб ![]() стало хибним”, або “істинність одного висловлювання
стало хибним”, або “істинність одного висловлювання ![]() не може впливати на істинність другого висловлювання
не може впливати на істинність другого висловлювання ![]() ”.
”.
Отже, як основну аксіому логіки висловлювань, що виражає відношення порядку, можна використовувати клаузу 2.4.1.
Приклад 2.4.1. Довести аксіоматичним методом справедливість клаузи
![]() ,
, ![]() (2.4.2)
(2.4.2)
правилом відділення, “Modus Ponens”.
Розв’язання. Використовуючи тотожності логіки Буля, виконаємо еквівалентні перетворення заданої клаузи ![]() , отримаємо
, отримаємо ![]() ,
, ![]() , що згідно з 2.4.1 підтверджує справедливість клаузи
, що згідно з 2.4.1 підтверджує справедливість клаузи ![]() ,
, ![]() . Тобто якщо в процесі доведення істинності будь-якої складної клаузи вдалося звести її до клаузи 2.4.2, то необхідно вважати, що доведення відбулося.
. Тобто якщо в процесі доведення істинності будь-якої складної клаузи вдалося звести її до клаузи 2.4.2, то необхідно вважати, що доведення відбулося.
Приклад 2.4.2. Довести аксіоматичним методом справедливість гіпотетичного силогізму, який заданий такою кляузою:
[TEX]A\rightarrow B[/TEX], ![]() . (2.4.3)
. (2.4.3)
Розв’язання. Перенесемо ![]() вліво за символ метаімплікації і отримаємо таку клаузу:
вліво за символ метаімплікації і отримаємо таку клаузу: ![]() ,
,![]() ,
, ![]() . Скориставшись правилом відділення 2.4.2 , отримаємо
. Скориставшись правилом відділення 2.4.2 , отримаємо ![]() ,
, ![]() . Скориставшись другий раз правилом відділення 2.4.2 , отримаємо
. Скориставшись другий раз правилом відділення 2.4.2 , отримаємо ![]() ,
, ![]() , що підтверджує справедливість гіпотетичного силогізму, оскільки його виведення відповідає основній аксіомі логіки висловлювань 2.4.1.
, що підтверджує справедливість гіпотетичного силогізму, оскільки його виведення відповідає основній аксіомі логіки висловлювань 2.4.1.
Приклад 2.4.3. Довести аксіоматичним методом істинність така тавтології (аксіома А1): ![]() .
.
Розв’язання. Використовуючи істинні тотожності логіки Буля, виконаємо еквівалентне перетворення заданої тавтології ![]() й отримаємо відношення порядку
й отримаємо відношення порядку ![]() ,
, ![]() , яке наведене в 5.4.1, що і підтверджує справедливість тавтології
, яке наведене в 5.4.1, що і підтверджує справедливість тавтології ![]() – аксіома А1.
– аксіома А1.
Приклад 2.4.4. Довести аксіоматичним методом істинність такої тавтології (аксіома А2): ![]() .
.
Розв’язання. Використовуючи істинні тотожності логіки Буля, виконаємо еквівалентні перетворення заданої тавтології: ![]() ,
,![]() ,
,![]() .
.
Користуючись правилом відділення ![]() ,
, ![]() і ще раз правилом відділення, отримаємо відношення порядку
і ще раз правилом відділення, отримаємо відношення порядку ![]() ,
, ![]() , що і підтверджує справедливість тавтології
, що і підтверджує справедливість тавтології
![]() – аксіома А3.
– аксіома А3.
Приклад 2.4.5. Довести аксіоматичним методом істинність такої тавтології (аксіома А3): ![]() .
.
Розв’язання. Використовуючи істинні тотожності логіки Буля, виконаємо еквівалентні перетворення заданої тавтології ![]() ,
, ![]() , що еквівалентно клаузі
, що еквівалентно клаузі ![]() ,
, ![]() , відповідає 2.4.2 правилу відділення, і підтверджує справедливість тавтології
, відповідає 2.4.2 правилу відділення, і підтверджує справедливість тавтології ![]() та аксіоми А3.
та аксіоми А3.
Приклад 2.4.6. Користуючись аксіоматичним методом, довести істинність такої клаузи: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Розв’язання. Задану клаузу можна подати як клаузу
![]() ,
, ![]() ,
, ![]() . Використовуючи істинні тотожності Буля, виконаємо еквівалентні перетворення останньої клаузи і отримаємо
. Використовуючи істинні тотожності Буля, виконаємо еквівалентні перетворення останньої клаузи і отримаємо ![]() ,
, ![]() ,
, ![]() . Застосувавши логічний закон дистрибутивності, отримаємо
. Застосувавши логічний закон дистрибутивності, отримаємо ![]() ,
, ![]() .
.
Після логічного перетворення клауза матиме такий вигляд:
![]() ,
, ![]() , що відповідає правилу відділення і підтверджує істинність клаузи
, що відповідає правилу відділення і підтверджує істинність клаузи ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Приклад 2.4.7. Користуючись аксіоматичним методом, довести істинність клаузи ![]() ,
, ![]() ;
; ![]() .
.
Розв’язання. Виконуючи еквівалентні логічні перетворення, отримаємо
![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Застосовуючи закон дистрибутивності, маємо ![]() ,
,![]() ,
, ![]() ; А,
; А, ![]() ;
; ![]() ,
, ![]() , що відповідає правилу відділення і підтверджує істинність клаузи
, що відповідає правилу відділення і підтверджує істинність клаузи ![]() ,
, ![]() ;
; ![]()
Для зручності та наглядності доведення логічних висловлювань аксіоматичним методом посилки логічного висловлювання записують у стовпчик спеціальної таблиці, де зазначаються перетворювана форма даного висловлювання і метод її отримання.
Приклад 2.4.8. Довести істинність логічного висловлювання ![]() ,
,
![]() аксіоматичним методом.
аксіоматичним методом.
Розв’язання. Посилки логічного висловлювання заносимо в табл. 2.4.1 і
робимо над ними перетворення, використовуючи відповідні правила і закони.
Таблиця 2.4.1
|
Посилки, наслідок |
Тотожна формула |
Як отримана |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2, 3 і МР |
|
|
|
із закону контрапозиції |
|
|
|
4, 5 і МР |
Із табл. 2.4.1 випливає, що доведення істинності наслідку ![]() логічного висловлювання отримано шляхом перетворення логічної посилки
логічного висловлювання отримано шляхом перетворення логічної посилки ![]() на еквівалентну
на еквівалентну ![]() через закон контрапозиції, а також застосування правила “Modus ponens” для відповідних посилок заданого висловлювання.
через закон контрапозиції, а також застосування правила “Modus ponens” для відповідних посилок заданого висловлювання.
Приклад 2.4.9. Довести істинність логічного висловлювання ![]() ,
, ![]() аксіоматичним методом.
аксіоматичним методом.
Розв’язання. Посилки логічного висловлювання заносимо в табл. 2.4.2 і робимо над ними перетворення, використовуючи відповідні правила виведення.
Таблиця 2.4.2
|
Посилки, наслідок |
Тотожна формула |
Як отримана |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1, 2 і МР |
|
|
|
3, 5 і МР |
|
|
|
4, 6 і МР |
Із табл. 2.4.2 випливає, що доведення істинності наслідку ![]() логічного висловлювання отримано шляхом застосування правила “Modus ponens” для відповідних посилок заданого висловлювання.
логічного висловлювання отримано шляхом застосування правила “Modus ponens” для відповідних посилок заданого висловлювання.
Приклад 2.4.10. Довести істинність логічного висловлювання ![]() ,
, ![]() аксіоматичним методом.
аксіоматичним методом.
Розв’язання. Посилки логічного висловлювання заносимо в табл. 2.4.3 і робимо над ними відповідні перетворення.
Таблиця 2.4.3
|
Посилки, наслідок |
Тотожна формула |
Як отримана |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1, 3 і МР |
|
|
|
2, 5 і МР |
|
|
|
4, 6 і МР |
Із табл. 2.4.3 випливає, що доведення істинності наслідку К логічного висловлювання отримано шляхом застосування правила “Modus ponens” для відповідних посилок заданого висловлювання.
2.5. Конструктивний метод
Протилежним до аксіоматичного є конструктивний метод у логіці висловлювань, який ґрунтується на таблицях істинності. Для його розуміння побудуємо таблицю істинності для будь-якого одного прикладу. Нехай задана така легенда: “Експедитор сказав, що він бачив шофера в кімнаті відпочинку”. Ця кімната знаходиться поряд зі складом. Стріляли у складі. Шофер заявив, що він ніякої стрілянини не чув. Висновок: якщо експедитор каже правду, то шофер веде слідство до помилки; не можуть експедитор і шофер одночасно говорити правду.
Для висловлювань з легенди введемо такі позначення:
А = “Експедитор сказав правду”.
B = “Шофер відпочивав у кімнаті відпочинку”.
С = “Кімната відпочинку знаходиться поряд зі складом”.
D = “Шофер чув стрілянину”.
Е = “Шофер сказав правду”.
Посилки слідчого мають такі наповнення:
“Якщо експедитор сказав правду, то шофер знаходився в кімнаті відпочинку” ![]() .
.
“Якщо шофер знаходився в кімнаті відпочинку, то він повинен був чути все, що робиться у складі ” ![]() .
.
“Якщо шофер мав можливість чути, що робиться у складі, то він чув і стрілянину” ![]() .
.
“Якщо вірити шоферу, то він не чув стрілянини” ![]() .
.
Висновки слідчого мають такі наповнення:
“Шофер мене обманює за умови, що експедитор каже правду”![]() .
.
“Експедитор і шофер одночасно кажуть правду” ![]() .
.
“Шофер обманює, він знаходився в кімнаті відпочинку, яка дійсно розташована поряд зі складом, – це все так, але за умови, що експедитор сказав правду або що шофер знаходився у кімнаті відпочинку”:
![]() .
.
“Шофер обманює, він чув стрілянину, а кімната відпочинку дійсно розташована
поряд зі складом – це все так, але за умові, що експедитор сказав правду або
що шофер знаходився в кімнаті відпочинку”: ![]() .
.
Будуємо таблицю істинності, табл. 2.5.1, в якій під Р розуміють спільну причину всіх посилок Р1, Р2, Р3, Р4, тобто їх кон’юнкцію: ![]()
Таблиця 2.5.1
|
№ |
A |
B |
C |
D |
E |
P1 |
P2 |
P3 |
P4 |
P |
C1 |
C2 |
C3 |
C4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
0 |
X |
X |
X |
X |
X |
I |
I |
I |
I |
I |
I |
X |
I |
I |
|
1 |
I |
X |
X |
X |
X |
X |
I |
I |
I |
X |
I |
X |
X |
X |
|
2 |
X |
I |
X |
X |
X |
I |
X |
I |
I |
X |
I |
X |
I |
X |
|
3 |
I |
I |
X |
X |
X |
I |
X |
I |
I |
X |
I |
X |
X |
X |
|
4 |
X |
X |
I |
X |
X |
I |
I |
X |
I |
X |
I |
X |
I |
I |
|
5 |
I |
X |
I |
X |
X |
X |
I |
X |
I |
X |
I |
X |
X |
X |
|
6 |
X |
I |
I |
X |
X |
I |
I |
X |
I |
X |
I |
X |
I |
X |
|
7 |
I |
I |
I |
X |
X |
I |
I |
X |
I |
X |
I |
X |
I |
X |
|
8 |
X |
X |
X |
I |
X |
I |
I |
I |
I |
I |
I |
X |
X |
I |
|
9 |
I |
X |
X |
I |
X |
X |
I |
I |
I |
X |
I |
X |
X |
X |
|
10 |
X |
I |
X |
I |
X |
I |
X |
I |
I |
X |
I |
X |
X |
X |
|
11 |
I |
I |
X |
I |
X |
I |
X |
I |
I |
X |
I |
X |
X |
X |
|
12 |
X |
X |
I |
I |
X |
I |
I |
I |
I |
I |
I |
X |
X |
I |
|
13 |
I |
X |
I |
I |
X |
X |
I |
I |
I |
X |
I |
X |
X |
I |
|
14 |
X |
I |
I |
I |
X |
I |
I |
I |
I |
I |
I |
X |
I |
I |
|
15 |
I |
I |
I |
I |
X |
I |
I |
I |
I |
I |
I |
X |
I |
I |
|
16 |
X |
X |
X |
X |
I |
I |
I |
I |
I |
I |
I |
X |
I |
I |
|
17 |
I |
X |
X |
X |
I |
X |
I |
I |
I |
X |
X |
I |
X |
X |
|
18 |
X |
I |
X |
X |
I |
I |
X |
I |
I |
X |
I |
X |
I |
X |
|
19 |
I |
I |
X |
X |
I |
I |
X |
I |
I |
X |
X |
I |
X |
X |
|
20 |
X |
X |
I |
X |
I |
I |
I |
X |
I |
X |
I |
X |
I |
I |
|
21 |
I |
X |
I |
X |
I |
X |
I |
X |
I |
X |
X |
I |
X |
X |
|
22 |
X |
I |
I |
X |
I |
I |
I |
X |
I |
X |
I |
X |
I |
X |
|
23 |
I |
I |
I |
X |
I |
I |
I |
X |
I |
X |
X |
I |
X |
X |
|
24 |
X |
X |
X |
I |
I |
I |
I |
I |
X |
X |
I |
X |
X |
I |
|
25 |
I |
X |
X |
I |
I |
X |
I |
I |
X |
X |
X |
I |
X |
X |
|
26 |
X |
I |
X |
I |
I |
I |
X |
I |
X |
X |
I |
X |
X |
X |
|
27 |
I |
I |
X |
I |
I |
I |
X |
I |
X |
X |
X |
I |
X |
X |
|
28 |
X |
X |
I |
I |
I |
I |
I |
I |
X |
X |
I |
X |
X |
I |
|
29 |
I |
X |
I |
I |
I |
X |
I |
I |
X |
X |
X |
I |
X |
X |
|
30 |
X |
I |
I |
I |
I |
I |
I |
I |
X |
X |
I |
X |
X |
X |
|
31 |
I |
I |
I |
I |
I |
I |
I |
I |
X |
X |
X |
I |
X |
X |
Клауза є істиною, якщо істинні значення слідства С покривають всі істинні значення спільної причини Р, тобто істинні значення спільної причини утворюють підмножину істинних значень слідства. Ця необхідність виконується для наслідку С1, оскільки ![]() .
.
Оскільки ![]() , то тавтологія, складена з цих посилок, буде дорівнювати
, то тавтологія, складена з цих посилок, буде дорівнювати ![]() , а суперечність матиме вигляд
, а суперечність матиме вигляд
![]()
Якщо наслідок С1 замінити на С2, то у всіх зазначених випадках причинно-наслідкові відношення порушуються і клауза перетворюється в хибне метависловлювання.
Для наслідку С3 в рядках 8 і 12 із множини рядків ![]() , стоїть хибне значення, тому умовні причинно-наслідкові відношення не виконуються і С3 є хибним наслідком
, стоїть хибне значення, тому умовні причинно-наслідкові відношення не виконуються і С3 є хибним наслідком
![]()
Для наслідку С4 всі його позначення істинності покривають істинності спільної причини Р, тобто наслідок С4 є істинним висновком:
![]() .
.
У загальному випадку побудуємо всі спільні рядки подій. У нашому випадку таких рядків 6, вони відповідають 0, 8, 12, 14, 15, 16. Їх об’єднання дає граничний випадок умови виконання причинно-наслідкових відношень
![]()
![]()
Але це є ДДНФ, яка відповідає конкретній причині Р. Всі можливі покриття шести значень істинності дає множина істиннісних наслідків. Так, висновок ![]() покривають усі шість умов виконання причинно-наслідкових відношень і тому вони є істинні. Що стосується двох інших висновків
покривають усі шість умов виконання причинно-наслідкових відношень і тому вони є істинні. Що стосується двох інших висновків ![]() і
і ![]() , то вони не покривають усі шість умов виконання причинно-наслідкових відношень, і тому є хибними наслідками.
, то вони не покривають усі шість умов виконання причинно-наслідкових відношень, і тому є хибними наслідками.
Для знаходження істинних наслідків із заданих причин знайдемо мінімальну нормальну форму (МНФ), мінімальне і трансверсальне покриття.
Для знаходженням МНФ за відомими ДДНФ використаємо метод Вейча або Карно, внаслідок чого отримаємо таку МНФ:
![]() .
.
Мінімальне покриття – це покриття з найменшим числом термів, що є висновком С1. До нього входять два вирішальних висловлювання, пов’язаних із правдивістю касира А і правдивістю експедитора Е. Всі інші твердження В, С, D є другорядними і можуть виступати в результуючому висновку спільно з А і Е.
2.6. Метод доведення від супротивного
Цей метод доведення істинності висловлювання полягає в такому: допускають, що істинним є заперечення того висловлювання, яке необхідно довести (наслідок); потім через причини (посилки) намагаються дійти до суперечності. Якщо це відбулося, то досліджуване логічне висловлювання істинне, якщо ні – хибне.
Приклад 2.6.1. Довести істинність (хибність) логічного висловлювання ![]() методом від супротивного.
методом від супротивного.
Розв’язання. Для зручності доведення логічного висловлювання представимо його в такому вигляді:
![]()
![]()
[TEX]\underline{A\rightarrow D} [/TEX]
∆![]() ,
,
де символ ∆ позначає “ наслідок “.
Припустимо, що посилки істинні, а наслідок - хибний. Якщо наслідок хибний, тоді ![]() - хибне. Але якщо
- хибне. Але якщо ![]() - хибне, то C і D також хибне. Якщо C і D хибні, а посилки
- хибне, то C і D також хибне. Якщо C і D хибні, а посилки ![]() і
і ![]() істинні, то А і В також хибні. Але якщо А і В хибні, а посилка
істинні, то А і В також хибні. Але якщо А і В хибні, а посилка ![]() за умовою істинна, то ми дійшли до суперечності, з якої випливає, що дане висловлювання істинне.
за умовою істинна, то ми дійшли до суперечності, з якої випливає, що дане висловлювання істинне.
Приклад 2.6.2. Довести істинність (хибність) логічного висловлювання ![]() методом від супротивного.
методом від супротивного.
Розв’язання. Для зручності доведення логічного висловлювання представимо його в такому вигляді:
![]()
![]()
С____
∆![]()
Припустимо, що посилки істинні, а наслідок – хибний. Тоді С – істинне, а А – хибне. Але якщо А – хибне, а С – істинне, то перші дві посилки ![]() і
і ![]() будуть також істинні, і це не веде до суперечності. Тому дане логічне висловлювання – хибне.
будуть також істинні, і це не веде до суперечності. Тому дане логічне висловлювання – хибне.
Приклад 2.6.3. Довести істинність (хибність) логічного висловлювання ![]()
![]() методом від супротивного.
методом від супротивного.
Розв’язання. Для зручності доведення логічного висловлювання представимо його в такому вигляді:
![]()
![]()
А
D______
∆![]() .
.
Припустимо, що посилки істинні, а наслідок – хибний. Тоді C і D – хибні, а А – істинне. Але якщо А - істинне, то і В за умовою повинне бути істинним. А якщо це так, то посилка ![]() буде хибна, що призводить до протиріччя, з якого випливає істинність даного висловлювання.
буде хибна, що призводить до протиріччя, з якого випливає істинність даного висловлювання.
2.7. Метод резолюцій
У цьому методі для доведення істинності висловлювань використовують аксіоми порядку. Суть методу зводиться до того, що дві посилки диз’юнкти з протилежними термами завжди можливо склеїти в один остаточний диз’юнкт, у якому вже не буде протилежних термів, наприклад ![]()
де А і С – задовільні терми або цілі диз’юнкти з будь-яким набором термів, включаючи хибність; В і ![]() - задовільні терми. Якщо послідовно застосувати метод резолюцій до досліджуваної клаузи, то в результаті цього отримаємо зменшення числа букв, у тому числі й до їх повного зникнення.
- задовільні терми. Якщо послідовно застосувати метод резолюцій до досліджуваної клаузи, то в результаті цього отримаємо зменшення числа букв, у тому числі й до їх повного зникнення.
Метод резолюцій за своєю суттю заміняє аксіому порядку, оскільки вона сама може бути доведена в рамках методу резолюцій, наприклад:
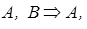
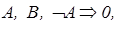
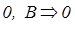 .
.
Необхідно відмітити, що посилка В тут не використовується. Це може бути допустимо, оскільки необов’язково використовувати всі посилки (їх число може бути збитковим) – головне в цьому отримання результату. При доведенні клаузи методом резолюцій необхідно її подати в нормальній кон’юктивній формі, а необхідною умовою доведення є отримання нуля, що є підставою істинності розглядуваної клаузи.
Приклад 2.7.1. Довести істинність клаузи 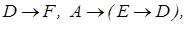
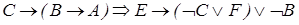 методом резолюцій.
методом резолюцій.
Розв’язання. Подамо клаузу в КНФ:
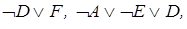
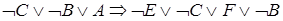 .
.
Перенесемо всі посилки в ліву частину клаузи
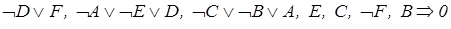 .
.
Випишемо посилки клаузи у стовпчик і склеїмо їх по черзі:
1. ![]() , 8.
, 8. ![]() (1, 2),
(1, 2),
2. ![]() , 9.
, 9. ![]() (3, 7),
(3, 7),
3. ![]() , 10.
, 10. ![]() (8, 9),
(8, 9),
4. Е , 11. ![]() (4, 10),
(4, 10),
5. С , 12. F (5, 11),
6.![]() , 13. 0 (6, 12).
, 13. 0 (6, 12).
7. В ,
Із черги склеювання посилок випливає, що ця клауза істинна.
Приклад 2.7.2. Довести істинність клаузи ![]()
![]() методом резолюцій.
методом резолюцій.
Розв’язання. Подамо клаузу в КНФ:
![]()
Перенесемо всі посилки в лівий бік клаузи:
![]()
Випишемо всі по порядку посилки клаузи і склеїмо їх по черзі:
1. ![]() , 8.
, 8. ![]() (2, 3), 15. 0 (11, 14).
(2, 3), 15. 0 (11, 14).
2. ![]() , 9.
, 9. ![]() (1, 8),
(1, 8),
3. ![]() , 10.
, 10. ![]() (4, 6),
(4, 6),
4. ![]() , 11.
, 11. ![]() (9, 10),
(9, 10),
5. ![]() , 12.
, 12. ![]() (5, 11),
(5, 11),
6. ![]() , 13.
, 13. ![]() (3, 12),
(3, 12),
7. ![]() , 14.
, 14. ![]() (7, 13),
(7, 13),
Із черги склеювання посилок випливає, що ця клауза істинна.



