• Нечітка логіка
  • 5.1. Основні визначення
  • 5.2. Операції над нечіткими множинами
  • 5.3. Поняття нечіткої і лінгвістичної змінної
  • 5.4. Нечіткі висловлювання та нечіткі предикати
  • 5.4.1. Основні логічні операції з нечіткими висловлюваннями
  • 5.5. Правило нечіткого логічного виводу
  • 5.5.1 Композиційне правило нечіткого виводу Заде

Нечітка логіка

Логіка в звичайному сенсі слова є уявленням механізму мислення, повинна бути завжди строго формалізованою. Однак в дійсності існує не одна логіка (наприклад, булева), а стільки, скільки ми побажаємо, тому що все визначається вибором відповідної системи аксіом. Звичайно, як тільки аксіоми прийняті, всі твердження, що побудовані на їх основі, повинні бути строгими, без протиріч пов'язані за правилами, встановленими в цій системі аксіом.

Нечітка логіка є узагальненням класичної логіки на випадок, коли істинність розглядається як лінгвістична змінна, що приймає значення типу: "дуже істинно", "більш-менш істинно", "не дуже хибно" і т.п. Зазначені лінгвістичні значення представляються нечіткими множинами. Основна відмінність від класичної логіки полягає в тому, що замість значень “ Істина “ і “ Хибність “ в нечіткій логіці використовується ступінь істинності, що приймає значення з нескінченної множини від 0 (Хибність) до 1 (Істина) включно. Отже логічні операції вже не можуть бути представленими таблицями істинності. У нечіткій логіці вони задаються функціями і лише в крайніх випадків - коли значення змінних виключно 1 або 0 - згадані вище функції дають таблиці істинності операцій класичної логіки.

Основи нечіткої логіки були закладені в кінці 1960-х років у працях відомого американського математика Лотфі А. Заде, що започаткував теорію нечітких множин. Термін "нечітка логіка" використовується зазвичай в двох різних значеннях. У вузькому сенсі, нечітка логіка - це логічне числення, що є розширенням багатозначної логіки. В її широкому сенсі, який сьогодні є переважаючим у використанні, нечітка логіка рівнозначна теорії нечітких множин. З цієї точки зору, нечітка логіка у вузькому сенсі є розділом нечіткої логіки в широкому сенсі.

5.1. Основні визначення

Означення 5.1.1. Нечіткою множиною з універсальної множини U називають сукупність упорядкованих пар = {(μ_х(а), а): а[TEX]\in [/TEX] U }, де μ_х(а) ‒ функція належності нечіткої множини (μ_х : U→[0, 1]), що приписує кожному елементу а[TEX]\in [/TEX] U ступінь його належності.

Використовують спеціальний запис нечітких множин. Якщо U є універсумом зі скінченою кількістю елементів, то можна представити так:

.                                            (5.1)

Якщо U є нескінченою множиною, то записують так:

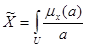.                                                                                              (5.2)

Знаки Σ і [TEX]\int_{}^{}  [/TEX] в формулах (5.1) та (5.2) мають інтерпретацію множини елементів. Мають місце також табличний та графічний спосіб представлення .

Приклад 5.1.1. Визначити за допомогою нечіткої множини поняття ”Людина середнього зросту ” , задавши універсум множиною U = {150, 155, 160,… 190} (зріст заданий у см).

Розв’язання. Виходячи з умови, з позицій першого дослідника, таке поняття може бути визначеним такою нечіткою множиною

.

Інший дослідник, вважаючи, що людина має середній зріст 175-180 см, представить шуканий результат іншою нечіткою множиною –

.

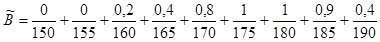Приклад 5.1.2. Введемо означення нечітких множин : - “ малий зріст людини ”, - “ середній зріст людини ”, - “ великий зріст людини ”. В якості універсуму застосуємо U = {xR : 0 ≤ x ≤ a_max}, де a_max– можливий максимальний зріст людини в см.

На рисунку 5.1 подано графіки функцій належності, що визначають уведені множини.

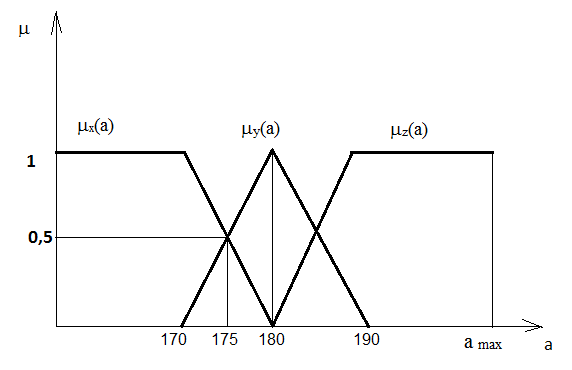
Рисунок 5.1 – Графіки функцій належності множин , , .

У точці а = 175 см, μ_x(a) =  μ_y(a) =0,5, тоді як  μ_z(a) = 0.

Функції належності зручно задавати в параметричній формі.Найбільшу популярність отримали трикутна, трапецевидна, гаусова, сигмоїдальна та Пі-подібна функції належності.

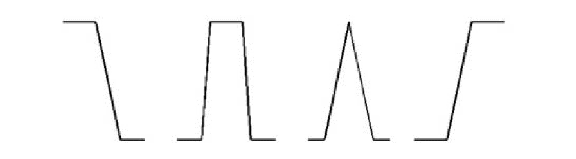
Рисунок 5.2 – Види графіків функцій належності (в порядку слідування: Z – функція; П - функція; Л - функція; S - функція).

Для побудови функцій належності можна використати метод, що базується на статистичній обробці думок групи експертів. У наведених вище прикладах використані прямі методи, коли експерт або просто задає для будь-якого а[TEX]\in [/TEX] U значення  μ_x(a), або визначає функцію належності. Як правило, прямі методи задання функції належності використовуються для вимірних понять, таких як швидкість, година, відстань, тиск, температура і так далі, тобто коли виділяються полярні значення.

Непрямі методи визначення значень функції належності використовуються у випадках, коли немає елементарних вимірних властивостей для визначення нечіткої множини. Як правило, це методи попарних порівнянь.

Означення 5.1.2. Висотою нечіткої множини називають величину .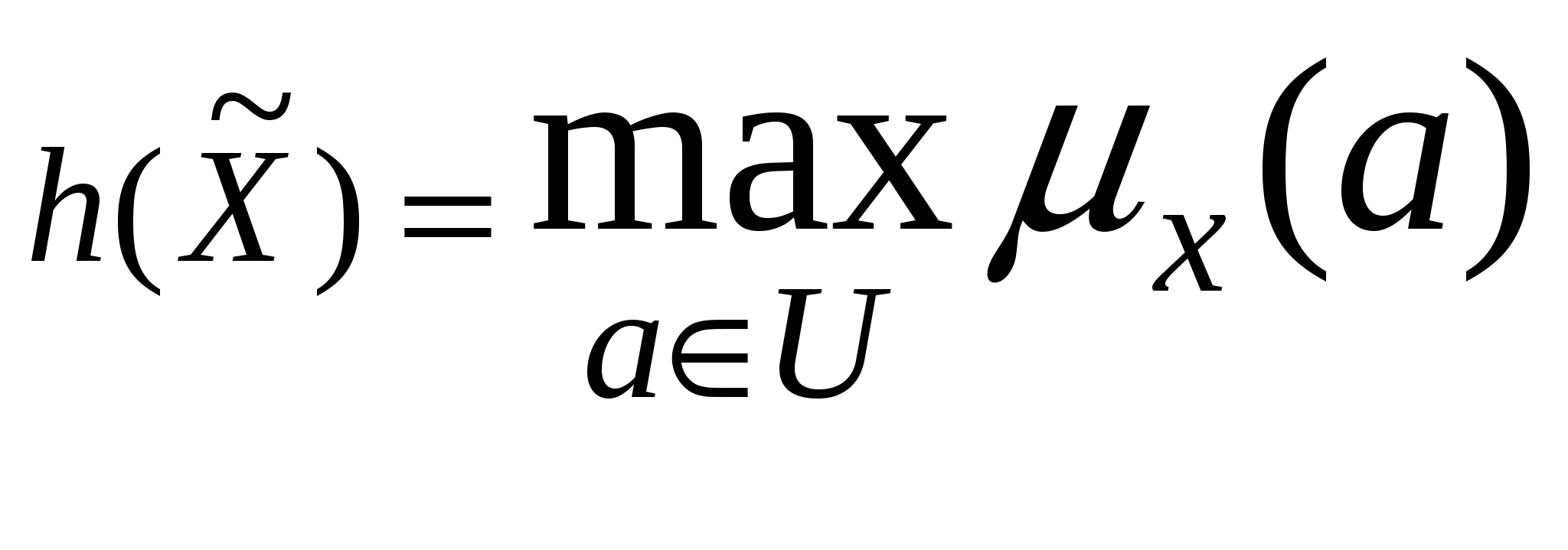

Приклад 5.1.3. Якщо U = {2, 3, 4, 5, 6}, a , то висотою нечіткої величини буде .

Означення 5.1.3. Нечітку множину називають нормальною, якщо . Якщо множина не є нормальною, то нормалізацію нечіткої множини можна провести за правилом , де вже стає нормальною нечіткою множиною.

Приклад 5.1.4. Нечітку множину прикладу 5.1.3 нормалізувати.

Розв’язання. За означенням 5.1.3 одержимо .

Означення 5.1.4. Нечітку множину називають субнормальною,

якщо h() < 1 .

Означення 5.1.5. Нечітку множину називають порожньою, якщо  μ_х(а) = 0 для всіх а[TEX]\in [/TEX] U.

Означення 5.1.6. Нечітка множина називається унімодальною, якщо  μ_х(а) = 1 лише для одного елемента з U.

Означення 5.1.7. α-перерізом нечіткої множини називають множину Х_α ={a[TEX]\in [/TEX]U: μ_х(а) ≥ α} (α[TEX]\in [/TEX][0,1]). Множина Х_α відноситься до звичайних (чітких) множин.

Приклад 5.1.5. Для заданої універсальної множини U = {0,1,2..,10} і нечіткої множини = визначити Х_0,6 і Х_1.

Розв’язання. Виходячи з означення 5.1.5 Х_0,6 ={4,5,6,7,8}; Х₁ ={5,6}.

Означення 5.1.8. Лінгвістичною змінною називається змінна, значеннями якої можуть бути слова або словосполучення деякої природної або штучної мови.

Означення 5.1.9. Терм-множиною називається множина всіх можливих значень лінгвістичної змінної.

Означення 5.1.10. Термом називається будь-який елемент терм-множини. В теорії нечітких множин терм формалізується нечіткою множиною за допомогою функції належності.

Приклад 5.1.6. Розглянемо змінну “швидкість автомобіля“, яка оцінюється за шкалою “низька“, “середня“, “висока“ і “дуже висока“.

У цьому прикладі лінгвістична змінна є “швидкість автомобіля“, термами - лінгвістичні оцінки “низька“, “середня“, “висока“ і “дуже висока“, які і складають терм-множину.

Означення 5.1.11. Фаззіфікацією називається процедура перетворення чітких даних в нечітку множину.

Не вдаючись у подробиці, процедура фаззіфікації виявляється в формалізації даних, як лінгвістичних змінних, введення всіх можливих термів, що їх характеризують, та побудові функцій належності для кожного терму.

Означення 5.1.12. Дефаззіфікацією (в нечіткій логіці) називається процедура перетворення нечіткої множини в чітке число.

В теорії нечітких множин процедура дефаззіфікації аналогічна знаходження характеристик становища (математичного очікування, моди, медіани) випадкових величин в теорії ймовірності. Наприклад, таким числом може стати максимум функції належності, центр ваги функції належності, чи щось інше.

5.2. Операції над нечіткими множинами

Визначення нечітких теоретико - множинних операцій можуть бути узагальнені зі звичайної теорії множин.

Означення 5.2.1. Дві нечіткі множини і , що задані на U, є рівними, якщо вони складаються з одних і тих же елементів для всіх x [TEX]\in [/TEX] U та μ_A(x)= μ_B (x). Позначають як = .

Означення 5.2.2. Дві нечіткі множини і доповнюють одна одну, якщо μ_A(x)= 1 - μ_B (x) для всіх x [TEX]\in [/TEX] U

Означення 5.2.3. Перетином двох нечітких множин і є така множина =, що складається з елементів для всіх x [TEX]\in [/TEX] U, що одночасно належать і з функцією належності μ_D(x)= min(μ_A(x), μ_B (x)).

Означення 5.2.4. Об’єднанням двох нечітких множин і є така множина =, що складається з елементів для всіх x [TEX]\in [/TEX] U, що належать або з функцією належності μ_D(x)= max(μ_A(x), μ_B (x)).

Означення 5.2.5. Різницею двох нечітких множин і є така множина = - , що складається з елементів для всіх x [TEX]\in [/TEX]  U, що мають функцію належності μ_D(x)= μ_A(x) - μ_B (x), якщо μ_A(x)> μ_B (x)), інакше μ_D(x)= 0.

На рис. 5.3 представлені графічно основні операції над нечіткими множинами: а) [TEX]\subset [/TEX]​ ; б) = 1 - ; в) [TEX]\frown[/TEX]​ г) [TEX]\smile[/TEX]​ .

Означення 5.2.6. Декартовим добутком хдвох нечітких множин і , визначених відповідно на універсамах U₁ та U₂, є нечітка множина пар (кортежів), визначених U₁ та U₂з функцією належності μ_D(x)= min(μ_A(x), μ_B (x)). Тобто =х = {( min(μ_A(x), μ_B (x)), (a,b) ): a[TEX]\in [/TEX] U₁ ,b[TEX]\in [/TEX] U₂ }.

Приклад 5.2.1. Для заданих нечітких множин

,

знайти [TEX]\frown[/TEX]​  та [TEX]\smile[/TEX]​ .

Розв’язання. За означеннями 5.2.4 та 5.2.5 знаходимо

[TEX]\frown[/TEX]​ = ,

[TEX]\smile[/TEX] = .

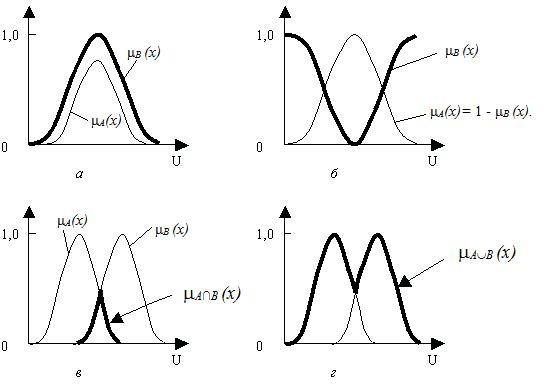
Рисунок 5.3 – Операції над нечіткими множинами.

Аналогічно операціям на чітких множинах, вводиться поняття нечіткого відношення.

Означення 5.2.7. Нечітким відношенням між множинами і називається підмножина їх декартового добутку, тобто [TEX]\subset [/TEX]х .

5.3. Поняття нечіткої і лінгвістичної змінної

При описі об'єктів та явищ за допомогою нечітких множин використовують поняття нечітких і лінгвістичних змінних.

Означення 5.3.1. Нечіткою змінною називають змінну, яка характеризується трійкою [TEX]\langle x,U,\tilde{A}\rangle  [/TEX] , де x ‒ ім'я змінної; U ‒ універсальна множина (область визначення x); ‒ нечітка множина на U, що описує функцію належності змінної.

Означення 5.3.2. Лінгвістичною змінною називають змінну, яку можна описати набором даних [TEX]\langle x,T,U,G,M\rangle [/TEX], де x ‒ ім'я лінгвістичної змінної, Т ‒ терм-множина (сукупність значень змінної), кожний елемент якої (терм) є нечіткою множиною, U – універсальна множина, G ‒ синтаксична процедура (правило), що породжує терми множини Т на U, М ‒ семантична процедура (правило), яка кожному терму задає функцію належності.

Приклад 5.3.1. Розглянемо лінгвістичну змінну з ім'ям “температура в кімнаті”. Тоді набір даних, що її характеризує можна визначити так:

Універсальну множину приймемо U = {x[TEX]\in [/TEX]N: 5 ≤ x ≤ 35}.

Терм-множину виберемо Т={“прохолодно”, “комфортно”, “жарко”}, в якій терми є нечіткими множинами з функціями належності:

,

,

.

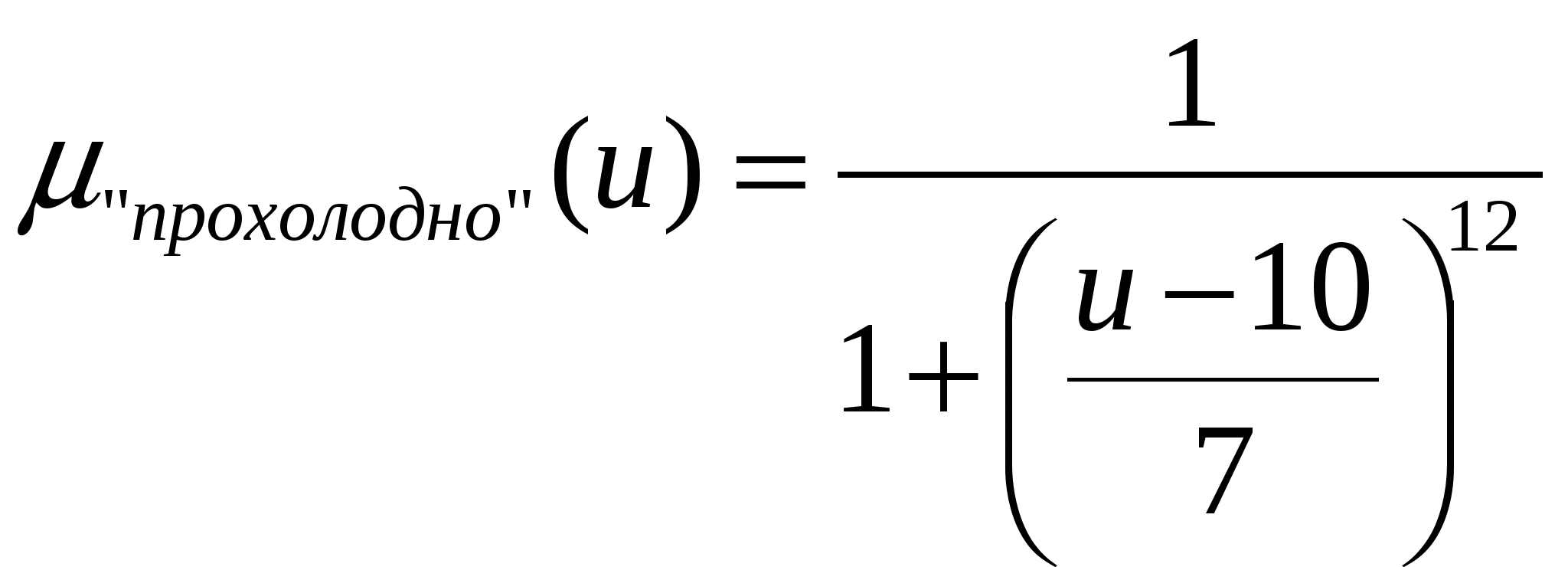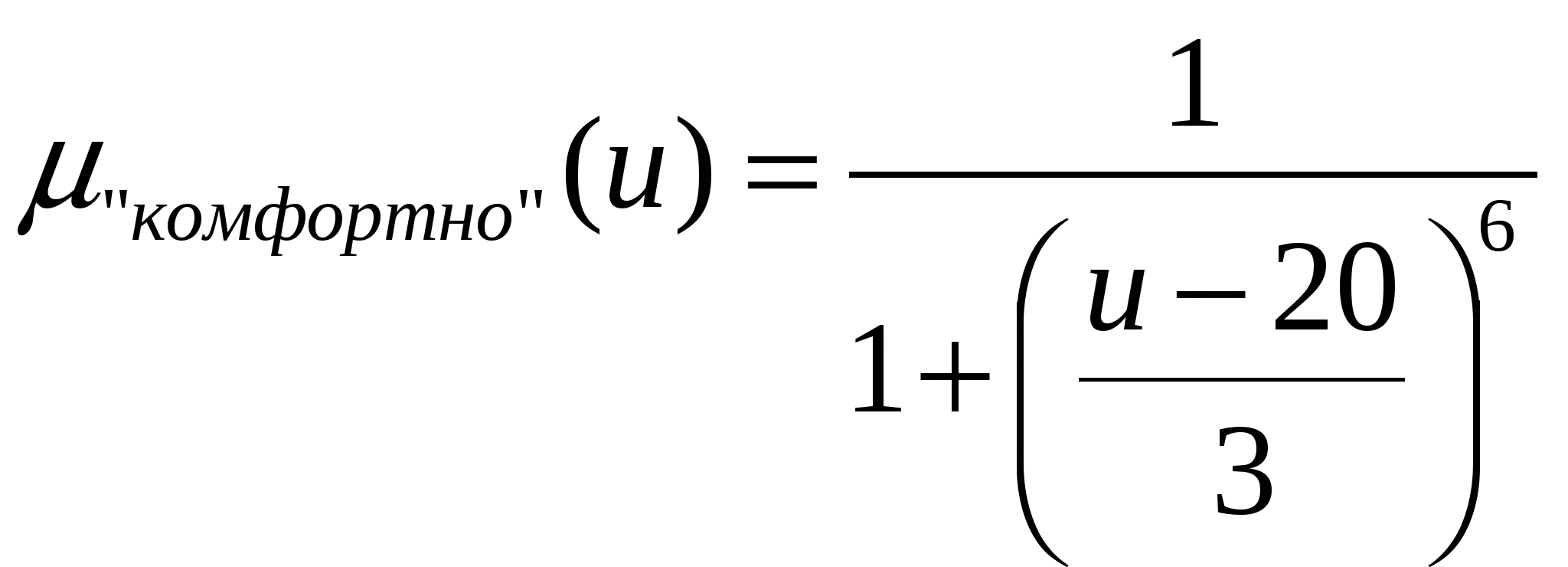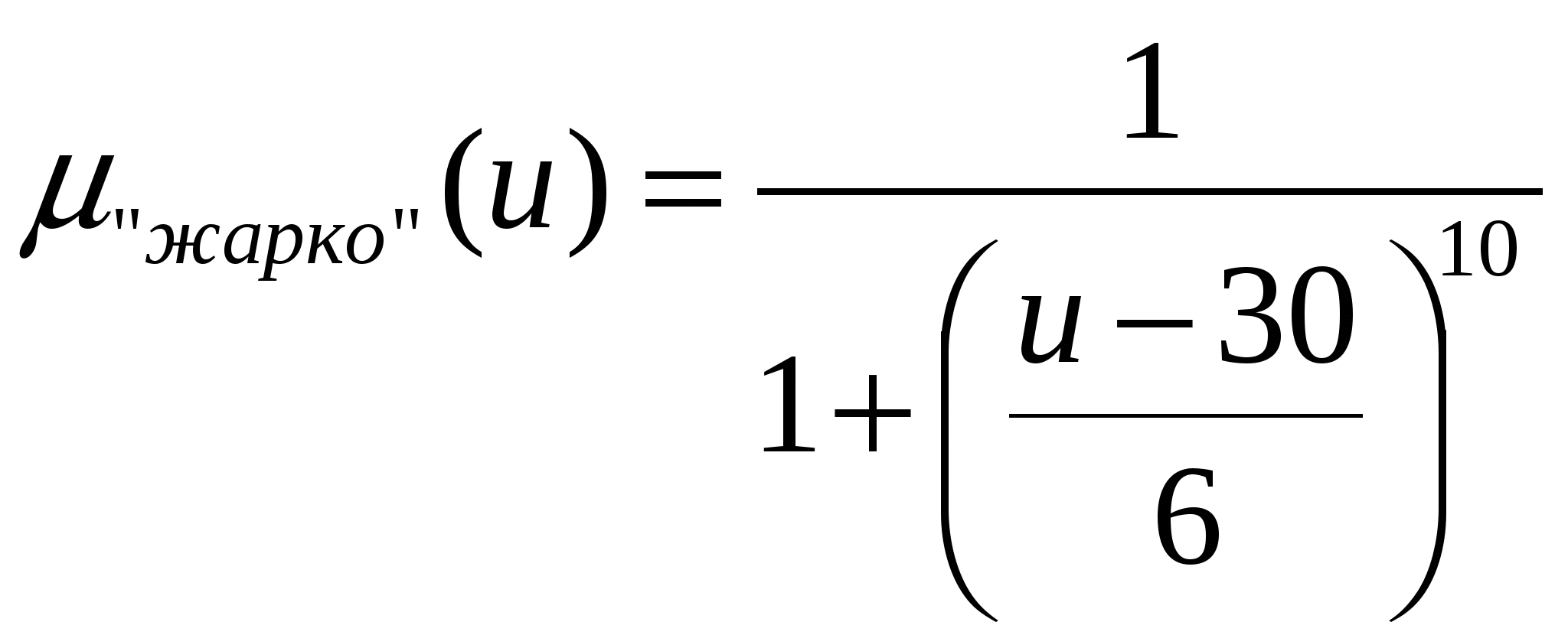3. Синтаксичні правила G, що породжують нові терми задамо за допомогою словосполучень (квантифікаторів) - “не”, “дуже”, “більш-менш”.

4. Семантичні правила М представлені в табл. 5.1.

Таблиця 5.1. Правила розрахунку функцій належності

Квантифікатор	Функція належності
Не t	1 - μt(u)
Дуже t	(μt(u))2
Більш-менш t

Графіки функцій належності термів “прохолодно”, “не дуже прохолодно”, “комфортно”,“більш-менш комфортно”,“жарко” та “дуже жарко” лінгвістичної змінної “температура в кімнаті” представлені на рис. 5.4.

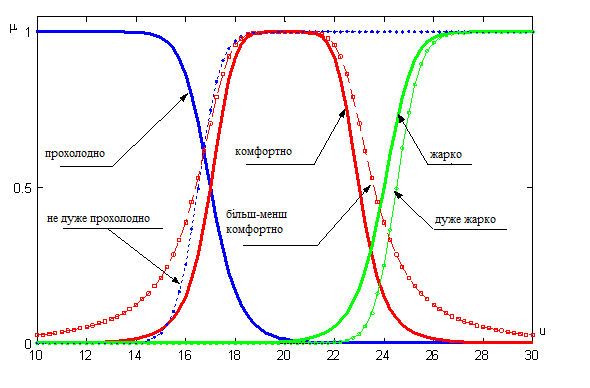
Рисунок 5.4 – Графіки належності термів лінгвістичної змінної.

5.4. Нечіткі висловлювання та нечіткі предикати

Поряд з поняттям нечіткої множини, Л. Заде запропонував узагальнення класичної логіки на основі розгляду нескінченної кількості значень істинності. Тобто, множина значень істинності висловлювань узагальнюється до інтервалу дійсних значень [0, 1], що дозволяє висловлюванню приймати будь-яке значення істинності з цього інтервалу. Це чисельне значення буде собою являти кількісну оцінку ступеня істинності висловлювання, що дозволяє побудувати логічну систему, в рамках якої виявилося можливим виконувати міркування з невизначеністю і оцінювати істинність висловлювань типу: “Швидкість автомобіля надмірно висока”, “Тиск в системі вельми значний”, “ Висота польоту літака гранично низька “ та ін. Вихідним поняттям нечіткої логіки є поняття елементарного нечіткого висловлювання.

Означення 5.4.1. Елементарним нечітким висловлюванням називається осмислений вираз звичайної мови, якому можна приписати значення істинності чи хибності тільки з деякою мірою впевненості.

Елементарні нечіткі висловлювання для зручності будемо позначати такими же літерами, що й нечіткі множини, й будемо ототожнювати з лінгвістичними змінними (див. означення 5.1.8, 5.3.2).

Приклад 5.4.1. Простий вислів “тиск великий” припускає, що лінгвістична змінна “тиск” має терм “великий”, для якого на універсальній множині U задається нечітка множина, яка визначається функцією належності.

Приклад 5.4.2. Нижче наводиться кілька прикладів елементарних нечітких висловлювань:

1. О. Бендер має досить високий зріст.

2. Завтра буде хмарно з проясненнями.

3. 3 - мале число.

4. Можливо, нам подадуть гарячу каву.

В цьому прикладі невизначеність нечітких висловлювань має різну природу. Невизначеність оцінки істинності у висловлюваннях 1,3 пов'язана з нечіткістю визначення понять “високий зріст” та “мале число”. Так, поняття “високий зріст” можна описати нечіткою множиною, щось на зразок з прикладом 5.1.1. Що стосується висловлювань 2 і 4, то тут окрім визначення нечітких змінних “похмура погода” і “гаряча кава” слід оцінити їх істинність відносно деякого моменту часу в майбутньому. Спільним для всіх цих висловлювань є та обставина, що значення їх істинності можна кількісно оцінювати дійсним числом з інтервалу [0, 1].

Для оцінки ступеня істинності довільної нечіткого висловлення зручно ввести в розгляд спеціальне відображення Т, що діє з множини нечітких висловлювань в інтервал [0, 1], тобто Т: →[0, 1]. Це відображення будемо називати відображенням істинності нечітких висловлювань. У цьому випадку значення істинності деякого нечіткого висловлення будемо позначати через T(). Так, якщо позначити нечітке висловлення 1 з прикладу 5.4.2 через , то його істинність формально може бути записана як Т(), а кількісно дорівнює, наприклад, 0,7, тобто Т() = 0,7.

Означення 5.4.2. Нечіткий предикат P(<x₁, x₂, …, x_k>) або, більш строго, k-місний нечіткий предикат, формально визначається як деяке відображення з декартового добутку універсумів Х₁, Х₂, ..., Х_k в деяку цілком впорядковану множину значень істинності, зокрема, в інтервал [0,1], тобто

Р: Х₁ × Х₂ × ... × Х_k → [0, 1].

За аналогією з звичайними (чіткими) предикатами, змінні x₁, x₂, ..., x_k називаються предметними змінними нечіткого предиката P (<x₁, x₂, …, x_k>), а декартовий добуток універсумів Х₁×Х₂×...×Х_k - його предметною областю.

Нечітке узагальнення логіки предикатів першого порядку, так само як і відповідні їй нечіткі числення, не знайшли широкого застосування при вирішенні прикладних завдань. Найбільш конструктивним напрямком в нечіткій логіці залишається використання нечітких висловлювань у формі означення лінгвістичних змінних. У цьому випадку нечіткі висловлювання можуть комбінуватися за допомогою нечітких логічних операцій або зв'язок, щось на зразок операцій над нечіткими множинами (див. розділ 5.2) .

5.4.1. Основні логічні операції з нечіткими висловлюваннями

Очевидно, що прийнятий в математичній логіці спосіб визначати логічні операції за допомогою таблиць істинності не може бути використаний в нечіткої логіки. Причина цього полягає в континуальної потужності множини значень істинності [0, 1]. Саме тому центральну роль у визначенні логічних операцій в нечіткої логіки набуває відображення істинності Т, яке має допоміжне значення в класичній математичній логіці.

Нехай - деяка множина елементарних нечітких висловлювань, а

Т: → [0, 1] - відображення істинності висловлювань.

Означення 5.4.3. Запереченням нечіткого висловлювання (записується як ¬ і читається “ не ”, "невірно, що») називається     унарна логічна операція, результат якої є нечітким висловлюванням, значення істинності якого за визначенням приймає значення:

T (¬) = l - T ().                                                                                                (5.3)

Приклад 5.4.3. Застосуємо операцію заперечення до нечіткого висловлювання - “О. Бендер має досить високий зріст” ( див. приклад 5.4.2). Висловлювання ¬ -“Неправильно, що О. Бендер має досить високий зріст” буде мати значення істинності T (¬) = I - T () = 1 - 0,7 = 0,3.

Означення 5.4.4. Кон'юнкцією нечітких висловлювань та (записується як: [TEX]\wedge [/TEX] і читається – “ і ”) називається бінарна логічна операція, результатом якої являється нечітке висловлювання, істинність якого визначається за формулою:

T([TEX]\wedge [/TEX]) = min{T(), T()}.                                                  (5.4)

Означення 5.4.5. Диз’юнкцією нечітких висловлювань та (записується як: [TEX]\vee [/TEX] і читається – “або ”) називається бінарна логічна операція, результатом якої являється нечітке висловлювання, істинність якого визначається за формулою:

T([TEX]\vee [/TEX]) = mах{T(), T()}.                                                             (5.5)

Означення 5.4.6. Нечіткою імплікацією або просто - імплікацією нечітких висловлювань і (записується як [TEX]\supset [/TEX]  і читається – “з слідує ”, “ЯКЩО , ТО ”) називається бінарна логічна операція, результат якої є нечітким висловлюванням, істинність якого може приймати значення, яке визначається за однією з наступних формул.

Нечітка імплікація Заде:

T([TEX]\supset [/TEX]) = max{min{T(), T()}, 1 - T()}.                                    (5.6)

Цю форму називають також класичною нечіткою імплікацією.

Нечітка імплікація Гьоделя :

T([TEX]\supset [/TEX]) = max{T(¬), T()}.                                                          (5.7)

Нечітка імплікація Мамдані :

T([TEX]\supset [/TEX]) = min{T(), T()}.                                                                 (5.8)

Нечітка імплікація Лукасевича:

T([TEX]\supset [/TEX]) = min{1, 1 - T() + T()}.                                                      (5.9)

Нечітка імплікація Гогена:

T([TEX]\supset [/TEX]) = min{1, T()/T() }, де T()>0.                                           (5.10)

Існують і інші способи обчислення нечіткої імплікації.

Нечітка імплікація відіграє важливу роль у процесі нечітких логічних умовиводів. Так само, як і в математичній логіці перший її операнд (нечітке висловлювання) називається засновком, а другий - висновком. Хоча класична нечітка імплікація знаходить найбільше застосування при розв'язанні прикладних задач і вона залишається справедливою у випадку звичайних висловлювань класичної логіки, інші способи обчислення нечіткої імплікації в окремих ситуаціях виявляються більш ефективними.

Приклад 5.4.4.Розглянемо складене нечітке висловлення у формі нечіткої імплікації: "Якщо О. Бендер має досить високий зріст, то завтра буде хмарно з проясненнями", при цьому істинність входять до нього елементарних нечітких висловлювань дорівнює T() = 0,7 і T () = 0,2. Знайти значення істинності імплікації.

Розв’язання. Тоді істинність цієї нечіткої імплікації, обчислена за формулою (5.6), дорівнює Т([TEX]\supset [/TEX]) = 0,3, за формулою (5.8) - Т([TEX]\supset [/TEX])= 0,2, за формулою (5.9) - Т([TEX]\supset [/TEX]) = 0,5, за формулою (5.10) - Т([TEX]\supset [/TEX]) =0,29.

 

5.5. Правило нечіткого логічного виводу

Основним правилом виводу в класичній логіці є правило modus ponens, згідно з яким ми можемо судити про істинність висловлювання В по істинності висловлювання А і імплікації А → В (див. розділ 2). Це правило виводить висновок ”B є істинно ”, якщо відомо, що “A є істинно ” і існує правило “Якщо A, то B” (A і B - чіткі логічні твердження). Нижче ми приведемо спосіб формалізації наближених міркувань, заснований на поняттях та операціях в нечіткій логіці.

Поняття нечіткого виводу займає центральне місце в нечіткій логіці і в теорії нечіткого управління. Цей процес включає в себе всі основні концепції теорії множин: функції належності, лінгвістичні змінні, методи нечіткої імплікації і т.д. Розробка й застосування систем нечіткого виводу включає в себе ряд етапів, реалізація яких виконується на основі положень нечіткої логіки, що розглянуті вище (рис. 5.5).

 

 

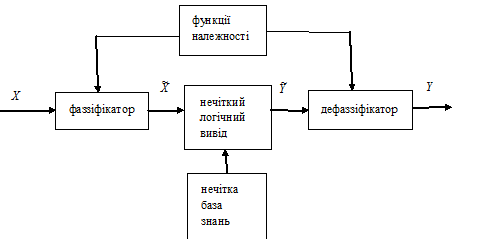
Рисунок 5.5 – Система нечіткого логічного виводу

Алгоритми нечіткого висновку розрізняються головним чином видом використовуваних правил, логічних операцій і різновидом методу дефаззіфікації. Розроблено моделі нечіткого висновку Мамдані, Сугено, Ларсена, Цукамото.

Означення 5.5.1. Нечіткою базою знань називається сукупність нечітких правил “Якщо – то”, що визначають взаємозв'язок між входами і виходами досліджуваного об'єкта.Узагальнений формат нечітких правил такий – “Якщо засновок правила, то висновок правила”.

Засновок правила або антецедент являє собою твердження типу “x є низький”, де “низький” -; це терм (лінгвістичне значення), заданий нечіткою множиною на універсальній множині лінгвістичної змінної x. Квантифікатори “дуже”, “більш-менш”, “не”, “майже” і т.п. можуть використовуватися для модифікації термів антецедента.

Висновок або наслідок правила являє собою твердження типу “y є d”, в якому значення вихідної змінної (d) може задаватися:

1. 1. нечітким термом: “y є високий”;
2. 2. класом рішень: “y є бронхіт”;
3. 3. чіткої константою: “y = 5”;
4. 4. чіткої функцією від вхідних змінних: “y = 5 +4 * x”.
5. Приклад 5.5.1. Наступна нечітка база знань описує залежність між віком водія (x) і можливістю дорожньо-транспортної пригоди (y):

“Якщо x = Молодий, то y = Висока”;

“Якщо x = Середній, то y = Низька”;

“Якщо x = Дуже старий, то y = Висока”.

Розв’язання. Представимо засновок нечітких правил лінгвістичною змінною х, що має 3 терми: “молодий”, “середній”,“дуже старий”, висновок – y (можливість ДТП) має терми “низька” і “висока”. Відповідні функції належності представлені на рис. 5.6.

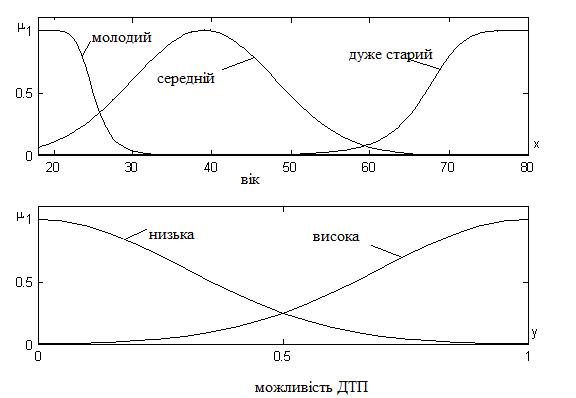
Рисунок 5.6 – Функції належності термів змінних x i y.

5.5.1 Композиційне правило нечіткого виводу Заде

Означення 5.5.2. Нечітким логічним висновком називається отримання висновку у вигляді нечіткої множини, відповідного поточним значеннях входів, з використанням нечіткої бази знань і нечітких операцій.

Означення 5.5.3. Композиційне правило виведення Заде формулюється таким чином: якщо відомо нечітке відношення між вхідними (x) і вихідний (y) змінними, то при нечіткому значенні вхідної змінної , нечітке значення вихідної змінної визначається так: , де - максмінна композиція.

Приклад 5.5.2. Дано нечітке правило “Якщо , то ” з нечіткими множинами і . Визначити значення змінної y на виході, якщо .

Розв’язання. Спочатку визначимо нечітке відношення між множинами, що відповідає заданому правилу, використавши означення 5.2.6, 5.2.7, та представимо його матрицею (Табл. 5.5.1).

Таблиця 5.5.1.

	5	10	15	20
1	0	0	0	0
2	0,1	0,1	0,1	0,1
3	0,5	0,5	0,4	0,2
4	0,8	0,8	0,4	0,2
5	1	0,8	0,4	0,2

Тепер за формулою  визначаємо нечітке значення y - .