• Алгоритмічні моделі
  • 12.1. Основні визначення
  • 12.2. Машини Тюрінга
  • 12.3. Нормальні алгоритми Маркова

Алгоритмічні моделі

12.1. Основні визначення

Точне визначення класу рекурсивних функцій разом із тезою Черча надає один із можливих варіантів уточнення поняття алгоритму. Проте це уточнення в цілому не пряме, оскільки поняття обчислювальної функції є вторинним по відношенню до поняття алгоритму. Виникає питання, чи не можна уточнити безпосередньо саме поняття алгоритму, а вже потім за його допомогою визначити точно клас обчислювальних функцій?

Основна ідея полягала в тому, що алгоритмічні процеси – це процеси, які може здійснювати відповідним чином влаштована “машина“. У зв’язку з розвитком сучасної обчислювальної техніки така алгоритмічна модель становить особливий інтерес, тому що в ній поняття алгоритму базується на командно-адресному принципі. Для наукового аналізу обчислювальних процесів, які можуть бути реалізовані машиною, бажано було знайти просту за своєю логічною структурою схему алгоритмічної машини, яка може бути предметом точної математичної теорії.

Відповідно до цієї думки вчені створили в точних математичних термінах “машинні моделі“ (математичні абстракції), на яких вдалось імітувати дію алгоритмів. Це було зроблено Постом і Тюрінгом у 1936-1937 рр. незалежно один від одного і майже одночасно із працями Черча. Пізніше, у 50-х роках двадцятого століття, до їх приєднався А. А. Марков. Алгоритмічні моделі цих вчених є претендентами на право бути основними формалізаціями поняття “алгоритм“. Це означає, що вони повинні бути універсальними, тобто в їх рамках можна описати будь-який алгоритм. Це дійсно так, тому що, по-перше, можна довести зведення однієї моделі до іншої, тобто будь-який алгоритм, описаний засобами однієї моделі, може бути описаний засобами іншої; по-друге, завдяки взаємному зведенню моделей у теорії алгоритмів удалося виробити інваріантну по відношенню до моделей систему понять, що дозволяє вести мову про властивості алгоритмів незалежно від того, яка формалізація обрана. Ця система понять базується на понятті обчислювальної функції, тобто для обчислення якої існує алгоритм.

Було доведено, що клас функцій, обчислюваних на цих машинах, збігається із класом рекурсивних функцій. Таким чином, це є ще одним підтвердженням тези Черча.

 

12.2. Машини Тюрінга

Перший важливий і достатньо широкий клас алгоритмів був уведений

А. Тюрінгом та Е. Постом у 1936-1937 рр. Алгоритми цього класу здійснюються особливими машинами, що називаються зараз машинами Тюрінга-Поста, або просто машинами Тюрінга. Машини Тюрінга копіюють в істотних рисах роботу людини і часто розглядаються як математичні моделі для вивчення функціонування людського мозку.

Машина Тюрінга – це математична модель, яка породжує обчислювальні процеси. Ідея машини Тюрінга базується на загальному аналізі процесів обчислення значень функцій обчислювачем. При цьому спостерігається основна гіпотеза теорії алгоритмів (теза Тюрінга) : будь-який алгоритм може бути реалізований у машині Тюрінга. Теза має сенс у тому, що кожна функція, для якої складений алгоритм знаходження її значень, представима машиною Тюрінга, тобто є обчислювальною.

Зафіксуємо два скінченних алфавіти – А = {a₀,a₁,…,a_n}, де n ≥ 0, і Q = ={q₀,q₁,…,q_m}, де m ≥ 1. При цьому А будемо називати зовнішнім алфавітом, а Q – внутрішнім алфавітом, або алфавітом станів. Додатково поставимо вимогу, щоб А ∩ Q =Ø і символи → , L, R не належать А[TEX]\smile [/TEX] Q. Один символ з А називають порожнім, зазвичай його позначають [TEX]\wedge [/TEX]. Усі інші букви з А називають непорожніми.

Візьмемо об’єднаний алфавіт B= А[TEX]\smile [/TEX] Q {→ , L, R}. Виділимо серед слів алфавіту В команди, які представляють слова одного з трьох видів:

1. q_ia_j → q_ka_l; 2) q_ia_j → q_kL; 3) q_ia_j → q_kR;

де 1 ≤ i ≤ m, 0 ≤ j ≤ n, 0 ≤ k ≤ m, 0 ≤ l ≤ n.

Ці команди читаються відповідно так:

1. перебуваючи у стані q_i і спостерігаючи символ a_j, перейти у стан q_k і написати символ a_l;

2. перебуваючи в стані q_i і спостерігаючи символ a_j, перейти у стан q_k і переміститися вліво на один символ ;

3. перебуваючи в стані і спостерігаючи символ, перейти у стан q_k і переміститися вправо на один символ .

Скінченна послідовність команд становить програму P із зовнішнім алфавітом А і внутрішнім алфавітом Q. У кожній команді програми виділимо її ліву частину – це підслово до символу “→“ і праву частину – підслово після символу “→“.

Означення 12.2.1. Машиною Тюрінга (МТ) називають упорядковану шістку { A, Q, a₀, q₀, q₁, P }, яка задовольняє такі умови:

1. множини А і Q скінченні, не перетинаються і не містять символів → , L, R;

2. a₀ [TEX]\in [/TEX] А, q₀ [TEX]\in [/TEX] Q, q₁ [TEX]\in [/TEX] Q. При цьому a₀ називається символом порожньої комірки, q₁ - початковий стан машини, q₀ - стан, у якому машина зупиняється;

3. Р – програма із зовнішнім алфавітом А і внутрішнім алфавітом Q, причому

а) програма не містить двох різних команд з однаковими лівими частинами;

б) будь-яка з команд не починається символом q₀.

Отже, МТ – це алгоритмічна модель, а не фізична машина. Проте для кращого розуміння роботи цієї машини її можна уявити у вигляді автоматичного пристрою ( див. рисунок).

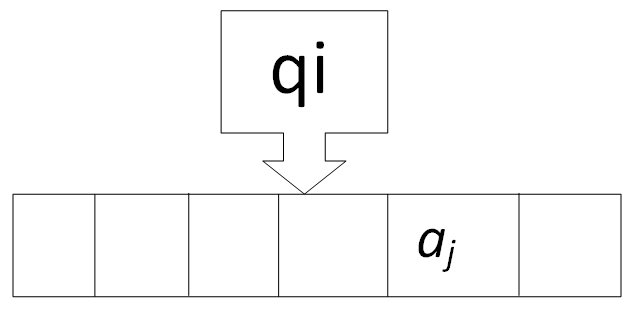
Пристрій оглядає стрічку, поділену на комірки, яку можна уявити необмеженою в обох напрямках. У кожний конкретний момент часу пристрій знаходиться в деякому стані q_i, спостерігаючи символ a_j, записаний в одній із комірок. Залежно від того, в якому стані перебуває пристрій ті який символ він спостерігає, пристрій здійснює дію, яка може полягати в тому, що пристрій на місце a_j запише a_l, а сам перейде в новий стан q_k (виконується команда першого виду), або переміститься вліво на одну комірку і змінить свій стан на q_k (виконується команда другого виду), або переміститься вправо на одну комірку і змінить стан на q_k (виконується команда третього виду).

Охарактеризуємо тепер роботу машини Тюрінга більш детально.

Означення 12.2.2. Машинним словом, або конфігурацією, називається будь-яке слово в алфавіті А[TEX]\smile [/TEX] { q_i }, для якого q_i[TEX]\in [/TEX] Q, причому символ q_iвходить у це слово один раз і не на останньому місці.

Приклад 12.2.1 Нехай задані алфавіти А={a₀, 1}, Q={q₀,q₁,q₂}.

Тоді слова a₀1a₀a₀q₁a₀ , a₀1q₂1, q₀111a₀ є конфігураціями, а слова a₀111q₁ , q₁1a₀q₂1a₀, a₀q₁q₁1 – до конфігурацій не належать.

У процесі роботи МТ здійснюється перехід від одного машинного слова до іншого. При цьому відбувається певне перетворення слів алфавіту А. Будемо говорити, що МТ перетворює машинне слово α в машинне слово γ

( записують МТ(α)= γ ), якщо існує скінченна послідовність слів γ₀, γ₁,…, γ_n , для яких виконуються умови :

1. γ₀ = α, γ_n = γ;

2. слово γ_і+1 одержане з γ_і дією МТ в один крок за визначеним правилом.

МТ може перетворити задане слово тільки в одне слово. Якщо МТ не перетворює слово α ні в яке слово, то говорять, що ця машина не застосовна до слова α, або значення МТ(α) не визначене.

Приклад 12.2.2. Знайти результат застосування МТ із зовнішнім алфавітом {a₀, 1,2}, внутрішнім алфавітом {q₀,q₁,q₂,q₃,q₄,q₅} і програмою q₁1→ q₂R , q₂2→ q₂1,q₂1→ q₃R, q₃2→ q₃R, q₃1→ q₄2, q₄2→ q₄R, q₄a₀→ q₅L, q₅2→ q₅L, q₅1→ q₅L, q₅a₀→ q₀R до слова 1221.

Розв’язання. Виходячи з початкової конфігурації q₁1221, знайдемо кінцеву конфігурацію, якщо вона існує. Маємо перетворення МТ за заданою програмою:

q₁1221→ 1 q₂221→1 q₂121→ 11 q₃21→112q₃1→112q₄2→1122q₄ a₀→112q₅2→11 q₅22→1 q₅122→ q₅1122→ q₅ a₀1122→ q₀1122.

Отже, слово 1221 МТ перетворює в слово 1122.

Значно складнішою, ніж задача застосування конкретних машин до конкретних слів, є задача створення МТ із наперед заданими властивостями.

Важливим класом МТ є машини, які обчислюють значення тих чи інших числових функцій для будь-якого набору значень аргументів із області визначення функції.

Нагадаємо, що числовою називають функцію f(x₁,x₂,…,x_n) , значеннями якої та значеннями її аргументів є невід’ємні цілі числа. Розглянемо часткові числові функції, визначені загалом не для всіх значень аргументів.

Означення 12.2.3. Функція називається обчислювальною за Тюрінгом, якщо існує машина Тюрінга, яка обчислює значення цієї функції для будь-якого набору значень аргументів із області визначення функції і не застосовна до наборів значень аргументів, що не входять до області визначення цієї функції.

Для обчислення числових функцій на МТ часто використовують спеціальне кодування чисел. Наприклад, невід’ємне ціле число m можна позначити словом (задати набором) з (m +1) одиниць, або скорочено 1^{m +1}. Тобто 0 задають як 1, 1 – як 11, 2 – як 111 тощо. Символом порожньої комірки буде слово 0. Тоді для побудови МТ буде достатньо зовнішнього алфавіту А={0,1}.

12.3. Нормальні алгоритми Маркова

Розглянемо ще один підхід до уточнення поняття алгоритму, запропонований російським математиком А. А. Марковим на початку 1950-х років. Досвід вивчення і застосування математики показує, що всі відомі алгоритми можна розбити на найпростіші кроки — елементарні операції. Як елементарну операцію, на базі якої побудовано нормальні алгоритми, А. А. Марков запропонував застосувати підстановку одного слова замість іншого.

Нормальні алгоритми Маркова (НАМ) перетворюють рядки, які задані у будь-якому скінченному алфавіті , у рядки у тому самому алфавіті.

Перейдемо до точних означень. Алфавітом будемо називати не порожню скінченну множину Е деяких символів. Символи “→ “ та “• “ не повинні належати алфавіту Е. Елементи алфавіту називатимемо також буквами. Слово в алфавіті Е — це скінченна, або порожня, послідовність його букв. Порожнє слово позначимо [TEX]\wedge [/TEX] . Множину всіх слів в алфавіті Е позначимо через Е*. Нехай Р, Q [TEX]\in [/TEX] Е*, тоді вирази Р →Q, Р→ •Q називаються відповідно формулами простої та заключної підстановки. При цьому перша з них означає, що замість Р потрібно вставити слово Q та перейти до наступної підстановки, а в другій формулі після підстановки процес закінчується.

Нехай Р→ ( •)Q означає будь-яку з формул підстановки (просту чи заключну). Нормальний алгоритм в алфавіті Е вважається заданим, якщо задана скінченна схема (таблиця) формул підстановок слів алфавіту Е

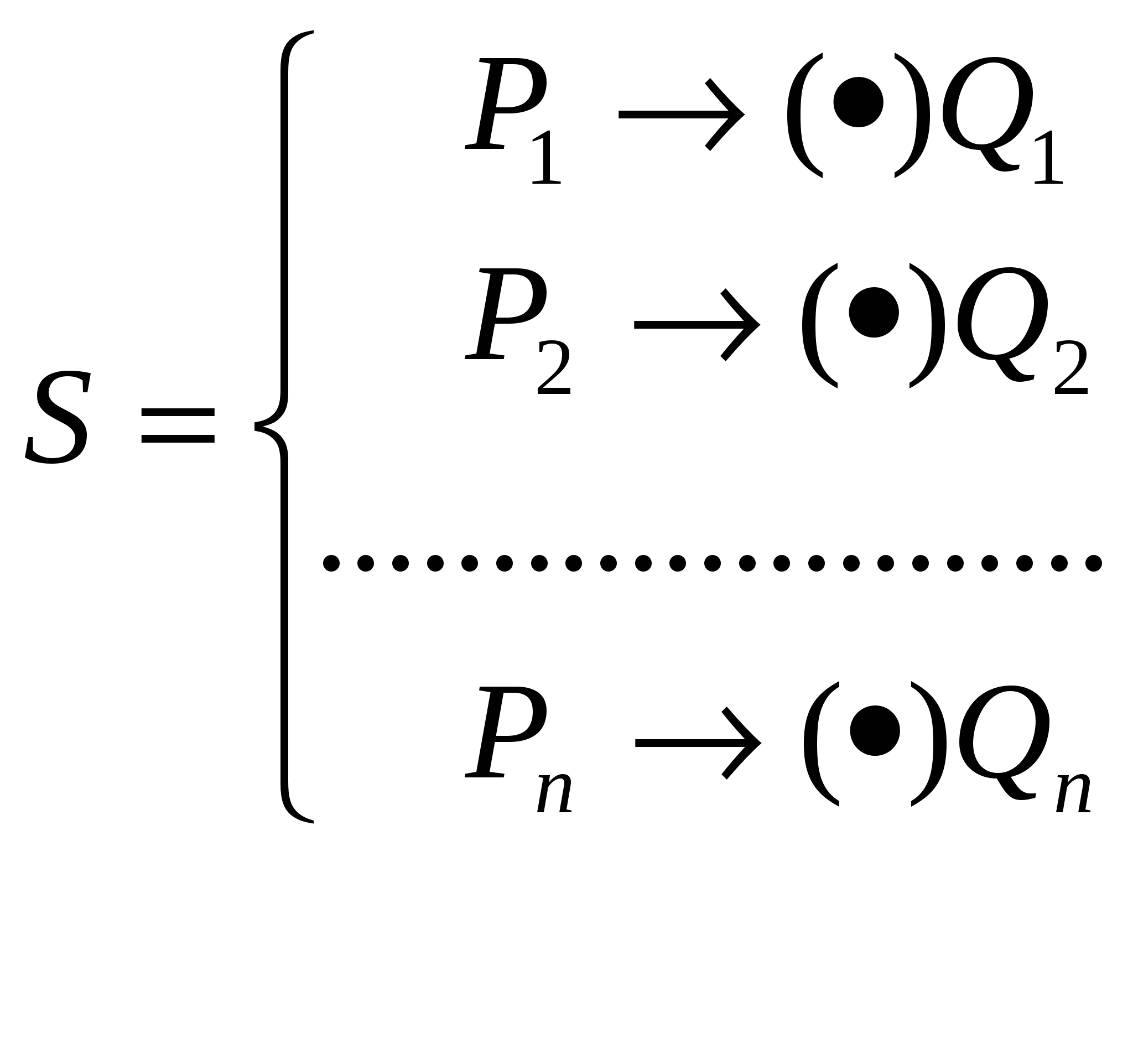                                                                                                                                                                                                               (12.3.1)

1. Означення 12.3.1. Нормальним алгоритмом Маркова (НАМ) в алфавіті Е називають пару{ Е,S}, яка складається з алфавіту Е та схеми S в цьому алфавіті.
2. Роботу нормального алгоритму Маркова можна описати у такий спосіб. Нехай задане слово α [TEX]\in [/TEX] Е*. Знаходимо першу в схемі S таку формулу підстановки α_i →( •)β_i, що α_iє підсловом α. Підставляємо в слово α слово β_i замість першого входження α_iв α. Нехай γ_i – результат цієї підстановки. Якщо формула підстановки виявилася заключною, тобто α_i → •β_i , то робота алгоритму закінчується і А(α) = γ_i. Якщо формула підстановки виявилась простою, тобто α_i → β_i, то до слова γ_i застосовуємо той самий пошук, який застосовувався до слова α і так далі. Якщо врешті-решт одержимо таке слово γ_i, що жодне із слів α₁, α₂, … α_n не входить в γ_i як підслово, то робота алгоритму закінчується і А(α) = γ_i . Якщо описаний процес не закінчується ніколи, то говоримо, що алгоритм А не застосовний до слова α.
3. Приклад 12.3.1. Розглянемо алгоритм який заданий у алфавіті Е={a,b} схемою підстановок :

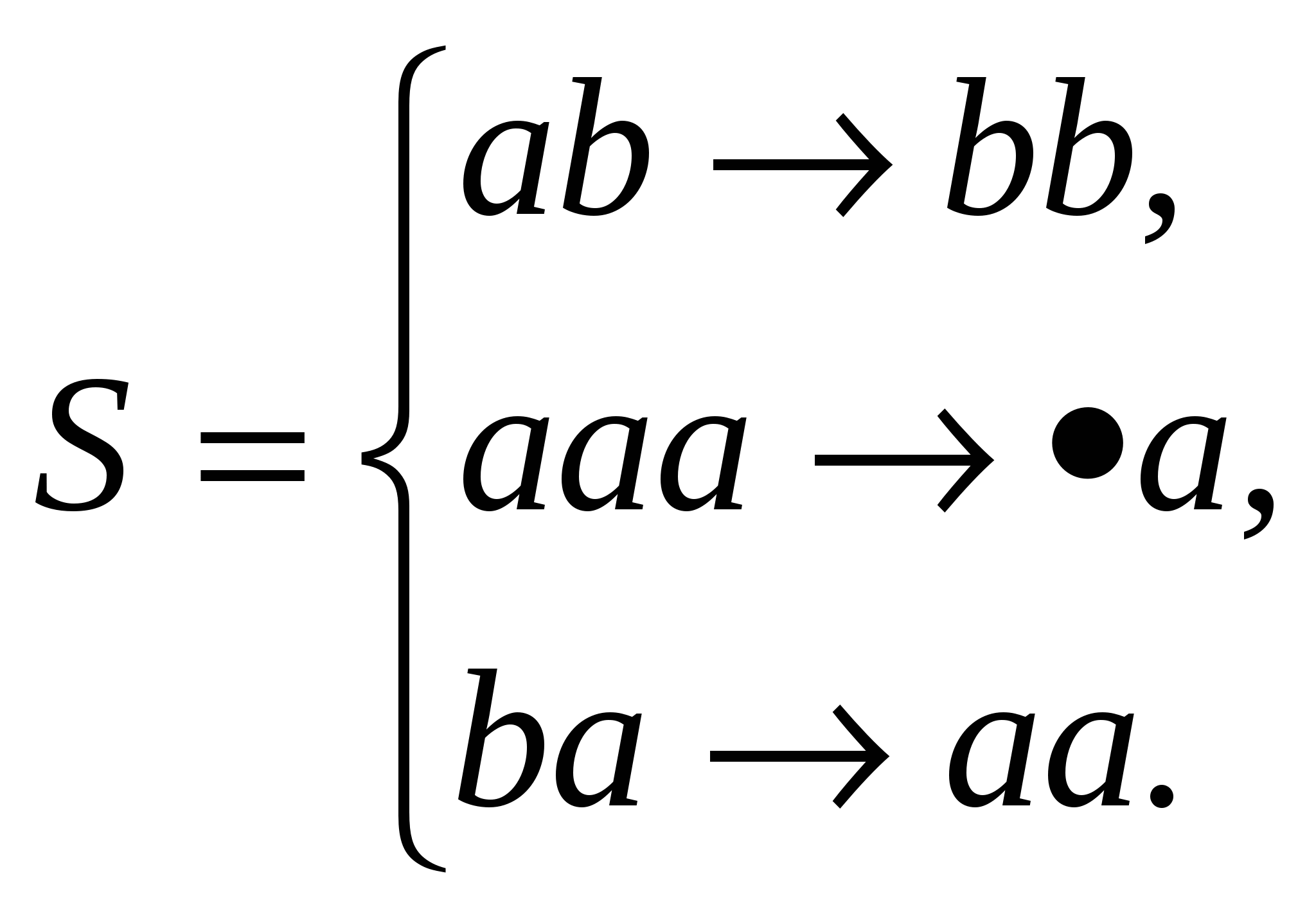(12.3.1)

Застосуємо його дію до слова Х = abba.

Першою підстановкою зі слова “abba“ одержимо слово Х₁ = bbba. Далі перша і друга підстановка до слова Х₁не діє, за третьою підстановкою зі слова “bbba“ одержимо слово Х₂= bbaa, до якого застосовна лише третя підстановка, яка перетворює його у слово Х₃=baaa. До слова Х₃ застосовні друга і третя підстановки, причому спочатку повинна виконуватися друга підстановка, але оскільки вона є заключною, то після її дії процес перетворення слів закінчується. Отже, слово «baaa» переходить в слово Х₄ = =ba. Таким чином, А(abba) =ba.

Означення нормального алгоритму Маркова, на перший погляд, не свідчить про якусь універсальність цього поняття. Проте виявляється, що клас нормальних алгоритмів має досить широкі можливості, зокрема під час обчислення значень функцій.

Означення 12.3.2. Функція називається нормально обчислювальною, якщо існує такий нормальний алгоритм, який обчислює значення цієї функції для будь-якого набору значень аргументів із області визначення функції і не застосовний до наборів значень аргументів, що не входять до області визначення цієї функції.

Постає питання про клас функцій, які можна обчислювати за допомогою нормальних алгоритмів. З цього приводу А. А. Марковим була сформульована гіпотеза, що одержала назву принципу нормалізації Маркова.

Принцип нормалізації Маркова. Клас нормально обчислювальних функцій збігається з класом обчислювальних функцій.

Аналогічно тому, як не можна довести гіпотези Черча і Тюринга, неможливо довести і принцип нормалізації Маркова.