• Нумерації алгоритмів
  • 13.1. Попередні відомості
  • 13.1.1. Нумерація за Гьоделем
  • 13.1.2. Головні універсальні функції та множини
  • 13.1.3. Канторові нумерації кортежів натуральних чисел
  • 13.1.4. Нумерації Кліні та Поста
  • 13.2 Нумерація машин Тюрінга та частково - рекурсивних функцій
  • 13.3. S-m-n- теорема
  • 13.4. M – зведення та властивості злічених множин
  • 13.5 Теореми Кліні про нерухому точку

Нумерації алгоритмів

Теорію нумерації можна вважати новою самостійною галуззю математики, породженою теорією алгоритмів. Самостійність цієї нової галузі виправдовується наявністю в ній глибоких математичних результатів, як майже очевидних, так і абсолютно несподіваних і нетривіальних.

Узагалі нумерація - це відображення деякої підмножини множини натуральних чисел N на досліджуваний клас конструктивних об'єктів (формул, слів, матриць і т. п.). Під конструктивним об'єктом розуміють об'єкт, який може бути повністю описаний за допомогою деякої скінченної послідовності символів скінченного алфавіту.

Теорія нумерації - розділ теорії алгоритмів, у якому вивчаються властивості класів об'єктів, занумеровані за допомогою натуральних чисел. Надавши номери об'єктам (машинам Тюрінга, частково - рекурсивним функціям і т. д. ), зможемо в багатьох випадках отримати глибокі наукові результати про ці об'єкти. Ідея використання нумерації об'єктів для отримання різних тверджень про ці об'єкти належить К. Гьоделю.

Нумерація алгоритмів відіграє важливу роль у дослідженні та аналізі самих алгоритмів. Оскільки будь-який алгоритм можна задати у вигляді скінченного слова (подати у вигляді скінченної послідовності символів деякого алфавіту), а множина всіх скінченних слів у скінченному алфавіті зліченна, то множина всіх алгоритмів також зліченна. Це означає існування взаємно однозначного відображення між множиною натуральних чисел та множиною алгоритмів, тобто можливість присвоїти кожному алгоритму номер.

Нумерація алгоритмів є водночас і нумерацією всіх алгоритмічно обчислюваних функцій, причому будь-яка функція може мати нескінченну кількість номерів. Існування нумерації дозволяє працювати з алгоритмами так само, як із числами. Особливо корисна нумерація в дослідженні алгоритмів, що працюють з іншими алгоритмами.

Під час реалізації ідей нумерації виявилося, що деякі результати теорії алгоритмів є наслідком закономірностей теорії нумерацій.

 

13.1. Попередні відомості

Узагалі теорія нумерації призначена для вивчення загальних властивостей класів об'єктів, занумерованих за допомогою будь-яких конструктивних об'єктів. У ролі конструктивних об'єктів найчастіше виступають натуральні числа. Ними можуть також бути впорядковані пари або скінченні послідовності натуральних чисел, раціональні числа, алгоритми, але ірраціональні числа, нескінченні підмножини натурального ряду, функції f:N→N не є такими.

Ідея нумерації об'єктів нечислової природи натуральними числами та перенесення змістовних тверджень про ці об'єкти у сферу формальної арифметики натуральних чисел уперше були використані К. Гьоделем під час доведення теореми про неповноту арифметики Пеано. Надалі ці ідеї були використані для нумерації фундаментальних об'єктів теорії алгоритмів, таких як машина Тюрінга, частково - рекурсивних функцій та інше. Нумеризація цих класів об'єктів дозволила в багатьох випадках більш чітко з'ясувати природу цих об'єктів, виявити ряд їх важливих і нових властивостей.

До появи ЕОМ алгоритми у сферах своїх застосувань вважалися різними за природою. З ерою комп’ютеризації прийшло усвідомлення того, що будь-яку інформацію можна закодувати (читай подати) числами, наприклад застосуванням в ЕОМ двійкового алфавіту {0,1}, й переконання, що виконання будь-якого алгоритму зводиться до дій над числами на базі арифметики та елементарної логіки. Тому перші наукові праці з теорії нумеризацій, що з’явилися до появи ЕОМ, викликають захоплення.

Нехай А - довільна непорожня скінченна або зліченна множина. Нумерацією множини А називають сюр’єктивне функціональне відображення

ν: N →А. Однозначною нумерацією множини А називають ін’єктивне ( а отже, бієктивне) відображення ν: N →А.

Якщо ν: N →А – нумерація, то для довільного а[TEX]\in [/TEX]А знайдеться хоча б одне значення n[TEX]\in [/TEX]N, для якого ν(n) = A. Кожне таке n будемо називати ν- номером елемента а.

Позначимо елемент a [TEX]\in [/TEX] А з номером n через a_n. Тоді елементи нумерованої множини А можна подати у вигляді послідовності: a₀, a₁, a₂, ... У загальному випадку в цій послідовності можливі повторення, тобто рівності

a_i= a_j, при i [TEX]\neq [/TEX] j. Якщо дана однозначна нумерація, то таких повторень немає.

Нехай A-множина, що складається з конструктивних об'єктів. Множина A називається ефективно зліченною множиною, якщо існує однозначна нумерація ν: N → A така, що виконані дві умови:

• Існує алгоритм ϰ₁, що обчислює за елементом a[TEX]\neq [/TEX]  A його номер ν(a) =N.

• Існує алгоритм ϰ₂, що встановлює за номером n [TEX]\neq [/TEX] N елемент a[TEX]\neq [/TEX]  A з даним номером.

Нумерація ν називається в цьому випадку гьоделівською нумерацією, умови можемо виразити в такому вигляді: функції ν: N→A і ν^-1: A→N обчислювальні. Таким чином, φ: N →А - ефективна нумерація ⇔ φ^-1: А→N - кодування А на N.

Нехай α - довільний алгоритм, що переробляє об'єкти множини Х в об'єкти множини Y. Нехай φ₁ і φ₂ - гьоделівські нумерації множин Х і Y відповідно. Алгоритм α можна розглядати як процедуру обчислення функції

f: N → N

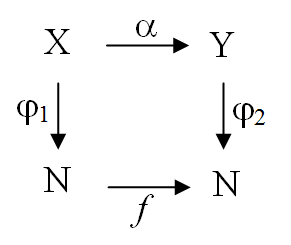
Якщо відображення φ: N → A є нумерацією множини А і φ (n) = a, то натуральне число n називається номером елемента a [TEX]\in [/TEX] А при нумерації φ.

Нижче введемо нумерації для об’єктів , що вивчаються в теорії алгоритмів. Синонімом терміна «нумерація» є термін «кодування» - спосіб задання об’єктів натуральними числами. По суті, кодування - частковий випадок нумерацій.

 

13.1.1. Нумерація за Гьоделем

К. Гьодель увів важливий метод арифметизації, в основі якого лежить однозначна нумерація об'єктів формальної системи (символів, термів, формул, доведень і т. д.) деякими натуральними числами. Ці числа були названі гьоделівськими номерами цих об'єктів. Кожному формальному символу, що входить в алфавіт системи, ставиться у відповідність деяке число, відношення та операції, визначені на словах, переходять у відношення та операції, визначені на номерах.

Нехай К – конструктивний простір – множина конструктивних об’єктів однакового виду. Очевидно, що К не більше ніж зліченна множина ( елементам К відповідає їх опис, що складається із слів скінченного алфавіту, а множина слів скінченного алфавіту є зліченною множиною).

Означення. Нумерація ν: N→К називається гьоделівською, якщо існує алгоритм, який дозволяє за записом будь-якого натурального числа одержати опис об’єкта, номером якого є це число.

Теорема 13.1. Нехай К – конструктивний простір ( не дорівнює Ø). Тоді :

1. існує гьоделівська нумерація простору К;

2. будь-яка гьоделівська нумерація простору К розв’язана;

3. будь-які дві гьоделівські нумерації простору К еквівалентні;

4. будь-яка нумерація простору К, еквівалентна гьоделівській, сама є гьоделівською.

Доведення наведеної теореми є предметом завдань для самостійного розв’язування.

Основна ідея, на якій базується нумерація за Гьоделем, полягає в тому, що будь - яке число N можна розкласти на прості множники :

,                                                                                                                                                                   (13.1)

що встановлює відповідність n - кам {a₁, a₂, …, a_n} номерів з N.

Нехай задано алфавіт зліченної множини A = {a₀,a₁, a₂, …}. Визначимо гьоделівські номери для кожної літери g(a_i) = 2i + 3, i ∈ N. Для кожного слова P= a_i0 a_i1…a_ik визначимо його гьоделівський номер:

, де p_k – k - е просте число. Послідовність формул (вона може становити і будь-які доведення) F₁, F₂,…, F_m одержить гьоделівський номер , де p_m – m –е просте число, G₁, G₂, …G_m – гьоделевські F₁,F₂,…F_m .

Відмінність нумерації за Гьоделем від інших нумерацій в тому, що множина номерів має «дірки», які частково заповнюються при збільшенні n. Цей «недолік» обертається перевагами під час нумерації виразів, що складаються не тільки з наборів цифр, а будь-якого тексту в будь-якому алфавіті.

Приклад 13.1. Занумерувати формулу ∀x(xxS(0) = x) у системі елементарної арифметики.

Розв’язання. Існують різні способи побудови гьоделівської нумерації для системи елементарної арифметики (ЕА). Виберемо 10 основних символів алфавіту теорії ЕА. Задамо відповідність цих символів натуральним числам за таблицею.

0	S	(	)	+	x	[TEX]\supset[/TEX]	¬	∀	=
1	2	3	4	5	6	7	8	9	10

 

Предметним змінним зіставимо прості числа, більші за 10 (наприклад x одержить номер 11, y – 12 і т. д.). Інші логічні зв’язки можна подати через [TEX]\supset[/TEX], ¬, ∀. Наприклад, A˅B ≡ ¬A[TEX]\supset[/TEX]B, [TEX]\exists [/TEX]xA(x) ≡ ¬∀x¬A(x).

Формула, що потребує нумерації складається з 12 символів, причому деякі входять в неї не один раз. Візьмемо перші 12 простих чисел, зведемо кожне з них у степінь, що дорівнює номеру відповідного символа й перемножимо одержані числа. Знайдене таким чином число й буде гьоделівським номером цієї формули :

2⁹⋅3¹¹⋅5³⋅7¹¹⋅11⁶⋅13²⋅17³⋅19¹⋅23⁴⋅29¹⁰⋅31¹¹⋅37⁴ =3512466963791134964962551783462053411408361516343794496506561501312862272000.

Отже, кожній формулі або послідовності формул можна поставити у відповідність єдине натуральне число. Не будь-яке число є гьоделівським номером, але будь-який гьоделівський номер однозначно визначає відповідний вираз.

 

13.1.2. Головні універсальні функції та множини

Означення. Функція U двох натуральних аргументів є універсальною для класу обчислюваних функцій одного аргументу, якщо для кожного n функція

U_n : x → U(n, x)                                                                                (13.2)

(«переріз» функції U при фіксованому n) є обчислюваною і якщо всі обчислювані функції (одного аргументу) трапляються серед U_n. (Нагадаємо, що ні функція U, ні обчислювана функція одного аргументу не мають бути обов’язково усюди визначеними).

Аналогічне визначення можна дати і для інших класів функцій (одного аргументу): наприклад, функція U двох аргументів буде універсальною для класу всіх всюди визначених обчислюваних функцій одного аргументу, якщо її перерізи U_n є всюди визначеними обчислюваними функціями одного аргументу і вичерпують усі такі функції.

Ключовим моментом у цьому сенсі є можливість ефективної нумерації обчислюваних функцій,

f₁(x), f₂(x), …, f_n(x), …,                                                                                                                                                   (13.3)

яка дозволяє вважати двомісну функцію

U(n, x) = f_n(x)                                                                                                                                                                   (13.4)

універсальною.

Теорема 13.2. Існує обчислювана функція двох аргументів, що є універсальною функцією для класу обчислюваних функцій одного аргументу.

Доведення. Запишемо всі програми, що обчислюють функції одного аргументу, в послідовність p₀, p₁, ...(наприклад, у порядку зростання їх довжини). Покладемо значення U (i; x) однаковому результату роботи i-ї програми при вході x. Тоді функція U і буде шуканою обчислюваною універсальною функцією. Переріз U_i буде обчислюваною функцією, що обчислюється програмою p_i.

Алгоритм, який обчислює саму функцію U, є, по суті, інтерпретатором для використовуваної мови програмування (він застосовує перший аргумент до другого, якщо ототожнити програму і її номер).

Означення. Нумерація і функція U(n, x) називаються гьоделівськими, якщо існує всюди визначена обчислювана функція s(n) така, що для будь-якої двомісної функції f(n, x) справедливе

f(n, x) = U(s(n), x).                                                                  (13.5)

Нехай F – деякий клас функцій від k - змінних. Функцію U(n, x₁,…,x_k) від змінних називають універсальною для класу F, якщо виконуються умови:

а) для будь-якого n[TEX]\in [/TEX]N

f_n(x₁, …, x_k) = U(n,x₁,…,x_k)[TEX]\in [/TEX]F;

б) для будь-якого f(x₁, …, x_k) [TEX]\in [/TEX] F існує n[TEX]\in [/TEX]N таке, що

f(x₁,…, x_k) = U(n,x₁,…,x_k).

Для множин використовується аналогічна термінологія.

Означення. Множину W [TEX]\subset [/TEX] N × N називають універсальною для деякого класу множин натуральних чисел, якщо всі перерізи

W_n = {x | (n, x) [TEX]\in [/TEX] W}

множини W належать цьому класу й інших множин у класі немає.

Іншими словами, це означає існування множини пар W = {(n, x) [TEX]\in [/TEX] W_n}, що в перерізі при фіксованому n визначають W_n.

Теорема 13.3. Область визначення універсальної функції U(n, x), а також множини пар {(n, U(n, x))} є гьоделівськими універсальними множинами.

 

13.1.3. Канторові нумерації кортежів натуральних чисел

Уведемо однозначні ефективні нумерації пар та n-ок натуральних чисел, які називаються канторовими нумераціями.

Нехай A = {(x, y) [TEX]\mid [/TEX] x, y [TEX]\in [/TEX] N}. Усі пари натуральних чисел розташуємо в послідовність так: пара (x, y) передує парі (u, v) ⇔ x + y< u + v або (x+y= u + v та x<y).

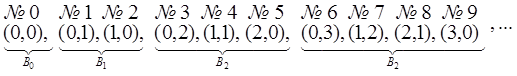                                                                (13.6)

Таку послідовність можна подати діагональним варіантом :

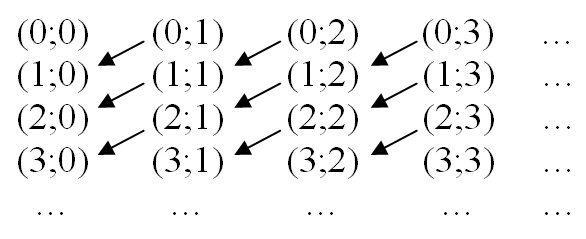
Пари (x; y) в даній послідовності виписані за блоками В₀, В₁, ... так, що в кожному блоці В_S поміщені пари (x; y) із заданою сумою: s = x + y.

Усередині блоку пари впорядковані за зростанням першої компоненти:

B_S = {(0; x+y), (1; x+y-1), … ,(x; y), … , (x+y), 0)}.

З наведених міркувань випливає: кожен елемент множини А має номер (номери починаються з нуля); для довільного натурального числа можна вказати відповідну пару (однозначно).

Номер пари (x, y) в такій послідовності позначають C(x, y) і називають канторовим номером пари (x, y) : С(1;0)=2, C(2;0)=5, C(0;3)=6, C(2;1)=8 і т. д.

Неважко переконатися, що C(x, y) = ( (x+y)² +3x +y) / 2                                                                                         (13.7)

Функція C(x, y) задає бiєкцiю NΧN→N. За допомогою цієї нумерації можна отримати нумерацію кортежів (трійок, четвірок і т. д.) натуральних чисел.

З формули (13.7) також випливає, що існують функції r, l такі, що належать класу загальнорекурсивних функцій і однозначно визначаються

C(x, y) = n, l(C(x, y)) = x, r(C(x, y)) = y,                                                                                                                           (13.8)

для будь-яких x, y ∈ N.

Зауважимо, що важливим є навіть не вигляд функцій l(n), r(n), а той факт, що вони є ефективно обчислювальні.

Використовуючи канторову функцію (13.7), можна визначити послідовність загальнорекурсивних функцій С₁, С₂, …,С_nтаку, що С_n– n - місна функція, що здійснює бієкцію Nⁿ → N.

Канторовими нумерувальними функціями називаються такі функції:

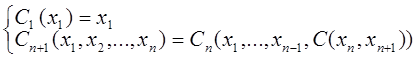,                                                                                                      (13.9)

в яких C(x,y) обчислюється за формулами (13.7). Наприклад,

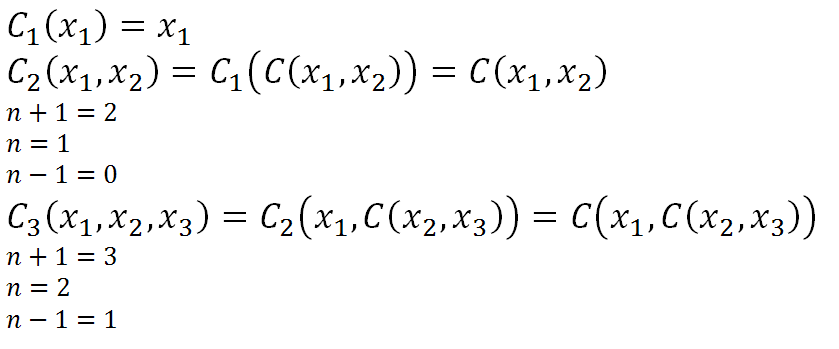
Приклад 13.2. Знайти номери впорядкованих трійок С₃(0,1,1) та С₃(1,1,1).

Розв’язання.

С₃(0, 1, 1) = C₂(0, C(1, 1)) = C(0, 4) = 10.

C(1, 1) = ( (1+1)² + 3+1) / 2 = 4; C(0, 4) = ( (0+4)² +0 + 4) / 2 = 10.

С₃(1, 1, 1) = C₂(1, C(1, 1)) = C(1, 4) = 16.

C(1, 1) = ( (1+1)2 + 3+1) / 2 = 4; C(1, 4) = ( (1+4)² +3 + 4) / 2 = 16.

 

13.1.4. Нумерації Кліні та Поста

Нумерації Кліні та Поста використовуються, в основному, в теорії рекурсивних функцій. Наведемо спосіб їх подання та означення.

Введемо стандартні позначення :

[x, y] = C(l(x), C(r(x),y)),                                                                                                                                                         (13.10)

де C(x, y) – канторів номер пари (x, y); l(x) та r(x) – відповідно ліве та праве числа пари С з номером x. З тотожностей

С(l(x), r(x)) = x, l(C(x, y)) = x, r(C(x, y)) = y та формули (13.6) випливає, що якщо [x, y] = n, то

x = C(l(n), l(r(n))), y = r(r(n)).                                                                                                                                                 (13.11)

Уведемо позначення [x]₂₁ = C(l(x), l(r(x))), [x]₂₂ = r(r(x)) і матимемо тотожності [[x]₂₁, [x]₂₂] = x, [[x, y]]₂₁ = x, [[x, y]]₂₂ = y, що вказують на взаємно однозначну нумерацію пар натуральних чисел. Отже, функція [x, y], також як і функція Кантора С(x, y), здійснює взаємно однозначну нумерацію пар натуральних чисел.

Функція K²(x₀, x₁) = U(l(x₀), C(r(x₀), x₁)) називається клініївською нумерувальною функцією. Ця функція визначається через головну універсальну функцію U(x, y), аргументи якої визначаються канторівською нумерувальну функцією С(x, y). Якщо f(x) = K²(m, x) для всіх x та деякого m, то це число m назвемо клініївським номером функції f.

Ставлячи кожному натуральному числу N у відповідність одномісну функцію K²(n, x), одержимо відображення множини натуральних чисел N на сукупність усіх одномісних частково - рекурсивних функцій Ч₁. Це відображення будемо називати нумерацією Кліні та позначати ϰ ( ϰ: N →Ч₁).

Переваги функції K²(n, x) не набагато принциповіші, хоча вони спрощують формули, що задають номери композицій функцій, суми та інших комбінацій рекурсивного характеру. Головним є те, що клініївська нумерація є гьоделівською.

Нумерація Поста зустрічається в теорії перелічуваних множин. Якщо S – перелічувана множина, то постівський номер цієї множини є клініївським номером функції                        f_n(x) = K²(n, x),                                                                                                                  (13.12)

множина значень якої збігається із S.

 

13.2 Нумерація машин Тюрінга та частково - рекурсивних функцій

Нехай задані зліченні множини символів A ={a₀, a₁, …, a_i, …} та Q = { q₀, q₁, …, q_j, …} }, що є зовнішнім алфавітом та алфавітом внутрішніх станів машини Тюрінга (МТ). При цьому a₀ інтерпретуємо як порожній символ (символ порожньої комірки), а q₀, q₁ – заключний та початковий стани МТ. Розглянемо множину {L, R, E, a₀, a₁, …, a_i, …, q₀, q₁, …, q_j, …} та проведемо її нумерацію за табл. 13.1.

Таблиця 13.1. Таблиця нумерації символів МТ.

	Символ	Код	Число нулів у коді
Символи зсуву	R	10	1
	L	100	2
	E	1000	3
Символи алфавіту стрічки	a0	10000	4
	a1	1000000	6
	…	…	…
	ai	100…00	2i+4
	…	…	…
Символи алфавіту станів	q0		5
	q1		7
	…	…	…
	qj	1000…000	2i+5
	…	…	…

 

Тоді команді I машини Тюрінга, що має вигляд qa → q′a′d , ставиться у відповідність двійковий набір вигляду

Код(I)=Код(q)Код(a)Код(q′)Код(a′)Код(d),                                                                                                                     (13.13)

в якому коди всіх літер приписані один поряд з іншим.

Упорядкуємо команди МТ відповідно до лексикографічного порядку лівих частин команд : q₁a₀, q₁a₁, …, q₁a_m,q₂a₀,…,q₂a_m,…,q_na₀,…,q_na_m .

Нехай задана відповідна послідовність команд. Тоді МТ поставимо у відповідність двійковий набір виду

Код(МТ)=Код(I₁)Код(I₂)… Код(I_n(m+1) ),                                                                                                                       (13.14)

який одержимо приписуванням один поряд з іншим кодів команд.

Приклад 13. 5. Нехай задана МТ A={a₀,a₁}, Q={q₀,q₁} з програмою :

q₁a₀→q₀a₀E ; q₁a₁→ q₀a₁E. Знайдемо код цієї машини.

Розв’язання. Використовуючи таблицю кодів ( див. табл. 13.1), маємо

Код(МТ) = 10⁷10⁴10⁵10⁴10³10⁷10⁶10⁵10⁶10³.

Бачимо, що в даному випадку МТ переводить конфігурацію q₁a₁^x у конфігурацію q₀a₁^x, то, подаючи натуральні числа у вигляді a₁ⁿ⁺¹ , одержимо, що МТ обчислює, по суті, функцію f(x) = x.

Зрозуміло, що вказане кодування є алгоритмічною процедурою. Маючи код МТ, можна однозначно відновити множину її команд (програму МТ). Для цього потрібно виділити півслова, що починаються з одиниці з нулями до слідкуючої одиниці. П’ятірка таких півслів утворює одну з команд.

Будемо розглядати код МТ як двійковий запис натурального числа. Дане число й назвемо номером МТ. Оскільки всі коди починаються з одиниці, то різним кодам відповідають різні числа. Впорядкуємо МТ за зростанням чисел, подаючи їх кодами, і занумеруємо їх

МТ₀, МТ₁, …,МT_n,…                                                                                                                                                         (13.15)

Таке упорядкування є ефективним у тому смислі, що існує алгоритм, який за номером n видає код (МТ_n), та існує алгоритм, який, навпаки, за кодом МТ_n видає n_MT.

Якщо через f(x) позначити одномісну функцію, яку обчислює машина Тюрінга МТ_n, то в результаті одержимо нумерацію всіх одномісних частково - рекурсивних функцій :

f₀(x), f₁(x), … ,f_n(x), …                                                                                                                                                         (13.16)

Аналогічно можна ввести нумерацію n - місних функцій.

 

13.3. S-m-n- теорема

S-m-n - теорема (також відома як лема про трансляцію, теорема параметрів, або теорема параметризації) належить до основних досягнень теорії алгоритмів ( гьоделівської нумерації обчислюваних функцій). Уперше була доведена Кліні у 1943 р..

Крім теоретичного, ця теорема має також застосування в практиці програмування. Теорема означає, що для заданої мови програмування та додатних цілих m та n існує певний алгоритм, який оперує кодом програм із m+n - вільними змінними. Цей алгоритм ефективно прив'язує m даних значень до перших m вільних змінних у програмі й залишає інші вільними.

Найпростішою формою, до якої застосовна теорема, є функція двох аргументів. Суть теореми в такому. Допустимо, що f(x,y) – обчислювальна функція. Для кожного фіксованого значення а змінної х функція f породжує одномісну обчислювальну функцію g_a(y) = f(a, y). З обчислювальності функції g_aвипливає існування такого індексу b , що f(a, y) = f_b(y). Зясовується, що індекс b можна ефективно обчислювати за параметром а.

Теорема 13.3.1 (s-m-n-теорема, проста форма). Нехай f(x,y) - обчислювальна функція. Існує всюди визначена обчислювальна функція S(x), така, що f(x, y) = f_s(x)(y).

Зауваження. Сформульовану теорему також називають теоремою параметризації, оскільки вона дозволяє за заданою обчислювальною функцією f(x,y) та фіксованим параметром а знайти гьоделівський номер s(a) програми, що обчислює функцію f_s(a)(y) = f(a, y).

Маючи дану гьоделівську нумерацію φ рекурсивних функцій, існує примітивно-рекурсивна функція s двох аргументів із такою властивістю: для кожного номера p часткової обчислюваної функції f із двома аргументами, та f(x,y) визначені для однакових комбінацій x- ів та y- ів однакові для тих комбінацій.

Теорема 13.3.2 (s-m-n-теорема). Для довiльних m, n>1 iснує (m+1) -арна РФ s(z, x₁, ..., x_m) така, що для всiх z, x₁, ..., x_т, у₁, ..., у_п маємо φ(x₁, ..., x_т, у₁, ..., у_п) = φ(у₁, ..., у_п).

Теорема 13.3.3 (s-m-n-теорема у спрощенiй формi). Для кожної ЧРФ f(x₁, ..., x_т, у₁, ..., у_п) iснує РФ s(x₁, ..., x_m) така, що для всiх x₁, ..., x_т, у₁, ..., у_п маємо f(x₁, ..., x_т, у₁, ..., у_п) = φ(у₁, ..., у_п).

При т=п=1 спрощена s-m-n-теорема збігається з 13.3.1.

Розглянемо приклади застосування s-m-n-теореми.

Приклад 13.6. Існує РФ s(x, y) така, що для всіх х, y, z[TEX]\in [/TEX]N маємо φ_s(x,y)(z)=φ_x(z)+φ_y(z).

Розглянемо функцію f(x, y, z)=φ_x(z)+φ_y(z). Функція f є ЧРФ, тому за

s-m-n-теоремою існує РФ s(x, y) така, що для всіх х, y, z[TEX]\in [/TEX]N маємо

f(x, y, z)=φ_s(x,y)(z)=φ_x(z)+φ_y(z).

 

13.4. M – зведення та властивості злічених множин

Надалі, в цьому розділі під множинами, якщо не обумовлено протилежне, ми будемо розуміти підмножини натурального ряду.

Означення. Множина A m - зводиться до множини B (позначається

A≤_m B), якщо існує обчислювана функція f: N → N така, що для будь-якого

x ∈ N справедлива еквівалентність x ∈ A ⇔ f (x) ∈ B.

Про функцію f говорять, що вона зводить множину А до множини В. Насправді потрібно було б говорити про зведення проблеми входження в множину А до проблеми входження в множину В.

Термін «m-зведення» історично походить з терміна «many-one-reduci-bility»; втім, як зазначає M. Сіпсер у своєму підручнику з теорії складності обчислень, замість цього краще говорити «mapping reducibility»(Зводиться за допомогою відображень), що також зберігає літеру m у позначенні.

Означення. Множина A одно-зводиться до множини B (позначається A≤₁ B), якщо існує ін 'єктивна обчислювана функція f: N → N така, що

x ∈ A ⇔ f (x) ∈ B для всіх x ∈ N.

Множина A називається m-еквівалентною (1-еквівалентною) множині B, якщо A ≤_m B і B ≤_m A (A ≤₁ B і B ≤₁ A).

Якщо множини A і B m-еквівалентні (1-еквівалентні), то ми пишемо

A ≡ _m B (A ≡ ₁ B). Неважко перевірити, що відношення ≡ _m є відношенням еквівалентності. Класи еквівалентності цього відношення називаються

m –степенями. Можна стверджувати, що всі множини з одного m –степеня «рекурсивні» ( або «нерекурсивні») однаковою мірою.

Нарешті, ми говоримо, що множини A і B зліченно ізоморфні (і пишемо A ≈ B), якщо існує обчислювана перестановка натурального ряду f така, що для будь-якого x ∈ N справедливе x ∈ A ⇔ f (x) ∈ B.

Інтуїтивно m-зведення - це спроба порівняти множини A та В.

Теорема 13.4.1. Справедливі такі твердження.

1. Будь-яка рекурсивна множина m – зводиться до будь-якої множини.

2. Якщо множина m – зводиться до рекурсивної множини, то вона рекурсивна.

3. Якщо множина m – зводиться до рекурсивно - зліченної множини, то вона рекурсивно - зліченна.

4. Будь - яка рекурсивно - зліченна множина m – зводиться до множини К.

 

13.5 Теореми Кліні про нерухому точку

Теорема Кліні про нерухому точку є основним інструментом дослідження в теорії рекурсивних функцій (РФ) та частково - рекурсивних функцій (ЧРФ). Він надає витончений і економічний метод поводження з конструкціями, що в іншому випадку вимагало б довгих і складних міркувань.

Ця теорема може бути наведена в декількох формах і може розглядатися з кількох точок зору. У певному сенсі теорема підсумовує певний клас діагональних методів. З іншого боку, ця теорема встановлює певний результат про нерухому точку і, подібно до теорем про нерухому точку з математичного аналізу, може бути використана для доказу існування багатьох неявно заданих функцій.

Теорема Кліні. Якою б не була обчислювана всюди визначена функція q(n), знайдеться таке n, при якому U(n, x) = U(q(n), x),

де U(n, x) - геделівська універсальна функція. Отже, завжди існує таке число n, що U_n = U_q(n) , тобто n і q(n) – номери однієї функції.

Теорема 13.5.1. Нехай f - (n+1) - арна РФ. Тоді існує n - арна РФ g така, що =для всіх значень x₁, ..., x_п.

Переформулюємо для випадку n=0.

Теорема 13.5.2. Нехай f(x) - РФ. Тоді існує nN таке, що _n = _f(n).

Первісне формулювання самого С. Кліні теореми про нерухому точку має такий вигляд:

Теорема 13.5.3 Нехай h(z, x) - ЧРФ. Тоді існує nN таке, що для всіх x маємо h(n, x)=_n(x).

Теорему Клiнi про нерухому точку краще називати теоремою про псевдонерухому точку. Насправді, умова _n=_f(n) зовсім не означає, що n = f(n), a свідчить тільки про те, що n та f(n) - індекси однієї i тієї самої ЧРФ.

Теорему про нерухому точку можна переформулювати і так:

Теорема 13.5.4. Нехай U (n; x) - головна обчислювана універсальна функція для класу обчислюваних функцій одного аргументу. Нехай V (n; x) - довільна обчислювана функція. Тоді функції U і V збігаються на деякому перерізі: знайдеться таке p, що U_p = V_p, тобто U (p; n) = V (p; n) для будь-якого n.

Приклад 2. Існує n[TEX]\in [/TEX]N таке, що для всiх x маємо φ_n(x)=2n+x³ⁿ.

Візьмемо функцію h(z, x)=2z+x^3z. За теоремою 7.4.3 iснує таке n, що для всiх x h(n, x)=φ_n(x). Отже, φ_n(x)=h(n, x)=2n+x³ⁿ для всiх x.

Приклад 3. Існує n[TEX]\in [/TEX]N таке, що D_n=E_n={n}.

Вiзьмемо функцiю h(z, x)= Така h є ЧРФ. За теоремою 7.4.3 iснує таке n, що для всiх x маємо h(n, x)=φ_n(x). Тоді φ_n(x)= Звідси D_п=Е_п={n}.

Теорема 13.5.5. Для кожної РФ f(x) існує строго монотонна РФ α(x) така, що для кожного n[TEX]\in [/TEX]N маємо φ_α(n) =φ_f(α(n)).

Наслiдок. Для кожної РФ f(x) та для кожного k[TEX]\in [/TEX]N існує n[TEX]\in [/TEX]N таке, що n>k та φ_n=φ_f(n).

Класичним прикладом застосування теореми про нерухому точку є такий її наслідок: існує програма, що друкує свій власний текст. В самому разі, якщо б такої програми не було, то відображення

р → (програма, що друкує при будь- якому вході р)

не мало б нерухомої точки. Формально цей факт можна виразити теоремою.

Теорема 13.5.6. Нехай U(n,x) – головна обчислювана універсальна для класу всіх обчислюваних функцій одного аргументу. Тоді існує таке число р, що U(р,x) = р для будь - якого x.

У термінах програмування на ЕОМ : нехай U(p,x) – результат застосування алгоритмічної програми р (складеній будь-якою мовою програмування) до стандартного входу х. Зрозуміло, що функція U буде головною універсальною функцією, тому, застосовуючи твердження теореми, одержимо програму р, що незалежно від входу на виході видасть р.