• NP - повні, складні та алгоритмічно нерозв’язні проблеми
  • 15.1. Розв’язні та нерозв’язні проблеми, NP- повнота, складність, зведення
  • 15.1.2. Приклади NP-повних задач
  • 15.2. Алгоритмічно нерозв’язні проблеми

NP - повні, складні та алгоритмічно нерозв’язні проблеми

15.1. Розв’язні та нерозв’язні проблеми, NP- повнота, складність, зведення

Теорія алгоритмів розподіляє всі проблеми, що потребують вирішення, на дві широкі категорії : алгоритмічно розв’язні та нерозв’язні. Останні проблеми будуть розглянуті дещо пізніше. Зупинимося на перших.

Бурхливий розвиток комп’ютерної індустрії підсвідомо наводить на думку, що вже не так важливо, які алгоритми застосовувати для розв’язної проблеми, - сучасний комп'ютер може все. Однак, наприклад, алгоритм «грубої сили» для розв’язування задачки на триста-п'ятсот змінних може зажадати такої кількості операцій, що набагато більше, ніж у Всесвіті елементарних частинок. Наприклад, якщо розв’язання задачі на найсучасніших комп'ютерах займе 10¹⁰ років, то очевидно, такий алгоритм для нас не має сенсу.

У попередньому розділі ми ввели поняття «складність алгоритму». Зрозумілим є бажання аналогічно визначити і складність завдання ̶ наприклад, як складність найефективнішого алгоритму, що розв’язує цю задачу (для даних розміру n). На жаль, це бажання нездійсненне. Доведено, що є завдання, для яких не існує найшвидшого алгоритму, тому що будь-який алгоритм для такого завдання можна «прискорити», побудувавши більш швидкий алгоритм, що розв’язує цю задачу. Це твердження називають теоремою Блюма про прискорення. Якщо відволіктися від технічних деталей, то спрощений варіант теореми Блюма можна сформулювати таким чином.

Теорема 15.1 ( теорема Блюма про прискорення). Існує така алгоритмічно розв’язна проблема Z, що будь-який алгоритм A, що вирішує цю проблему, можна прискорити таким чином: існує інший алгоритм А₁, що також вирішує Z і такий, що T _А1 (n) ≤ log T_A (n) для майже всіх n.

Зауважимо, що теорема Блюма не стверджує, що прискорення можливе для будь-якої задачі. Більше того, для деяких задач існує оптимальний (найшвидший) алгоритм. Однак твердження теореми Блюма про існування «незручних» задач не дозволяє визначити універсальне (застосовне до всіх задач) поняття «оптимального алгоритму».

Тому в теорії складності алгоритмічно розв’язних проблем використаний інший підхід  через класи складності.

Означення 15.1. Нехай f (n) - деяка функція, що відображає N в N. Клас складності C (f (n)) - це множина всіх задач, для яких існує хоча б один алгоритм, складність якого не перевищує O (f (n)).

Це визначення в певному сенсі умовне - позначення C(f (n)) ніколи не застосовують. Чому? Тому що для завдання реального класу задач необхідно ще уточнити:

• що ми розуміємо під «алгоритмом»;

• яка складність (тимчасова, ємнісна чи ще якась) нас цікавить.

При різних відповідях на ці питання одержимо різні класи завдань, і для кожного класу використовується спеціальне позначення.

Термінологія класів складності з 70-х років значно змінилася й поповнилася новими термінами, розширила рамки вже існуючих. Незмінними аспектами при побудові глобальної картини ієрархії складності залишаються такі.

• У теорії складності під «алгоритмом» зазвичай розуміють той чи інший різновид машини Тюрінга. Винайдення нових різновидів приводить до появи й нових класів складності. Наприклад, окрім уже відомих класів P, NP, NPC, з’явилися класи: EXPTIME (іноді має назву EXP) - задачі, які розв’язуються детермінованою машиною Тюрінга за O (2^p(n) ) часу, де р(n) є поліномом функції n; EXPSPACE - задачі, для розв’язання яких детермінованій машині Тюрінга потрібно O(2^p(n)) ємнісного простору, де р(n) є поліномом функції n; BPP – проблеми, розв'язні за допомогою ймовірнісної машини Тюрінга в поліноміальний час із похибкою ймовірністю не більше 1/3 та інші. Є й екзотичні класи, наприклад, P^NP- клас задач, що розв’язуються за поліноміальний час детермінованою машиною Тюрінга з оракулом для NP-завдання.

• Для формальних визначень класів складності зазвичай розглядають не довільні алгоритми, а алгоритми для так званих задач розв’язання (decision problem), у яких потрібно визначити, належить чи ні певний елемент деякій множині. Враховуючи необхідність кодування даних, що подаються на вхід машині Тюрінга, ці задачі абсолютно еквівалентні задачам розпізнавання мов, коли на деякому алфавіті ∑ розглядається підмножина слів L [TEX]\subset [/TEX]∑* і для довільного слова l ∈∑* потрібно визначити, чи належить воно мові L.

• У сучасній теорії складності обчислень поняття поліноміального алгоритму є адекватним математичним уточненням інтуїтивного поняття «ефективний алгоритм», а клас P становить «клас ефективно розв'язуваних задач». Тобто, прості задачі (розв'язувані) - це задачі, які розв’язування за поліноміальний час. Важкорозв’язні задачі - це задачі, які не розвязуються за поліноміальний час, або алгоритм розв'язання за поліноміальний час не знайдений.

• Побудовано ієрархічне співвідношення класів складності : P⊆NP⊆ BPP⊆ PH⊆ EXPSPACE⊆ EXPTIME, тобто одні містять у собі інші (більшість включень не доведено). Однак, зважаючи на потужності сучасних засобів обчислювальної техніки, задачі інших класів складності розглядаються поки що тільки в теорії, а однією з найбільш відомих відкритих проблем залишається питання про рівність класів P та NP.

У теорії складності обчислень одним із основних інструментаріїв, що застосовуються, є відомий науковий метод зведення - перетворення однієї задачі в іншу. У загальному випадку, якщо у нас є алгоритм, що перетворить екземпляри задачі P₁в екземпляри задачі P₂, які мають ту самому відповідь (так / ні), то говорять, що P₁ зводиться до P₂. Таким чином, зведення - це відношення між двома задачами. За допомогою такого зв'язку може бути доведена приналежність до того або іншого класу складності.

Зведення алгоритмічне - одне з основних понять теорії алгоритмів. Виникло у зв'язку з тим, що нерозв'язність (і розв'язність) багатьох алгоритмічних проблем встановлюється здебільшого не безпосередньо, а шляхом зведення до досліджуваної проблеми такої алгоритмічної проблеми, нерозв'язність якої вже доведена.

Поняття алгоритмічного зведення було уточнено А. Тюрінгом: якщо, деяка машина Тюрінга переробляє послідовність закодованих значень функції g у послідовність закодованих значень функції f, то функція f зводиться до функції g. Якщо f зводиться до g за Тюрінгом, f ≤ _T g, a g зводиться до f, g ≤ _T f, то кажуть, що f і g мають один і той степінь нерозв'язності, або f ≡ _T g.

Останнім часом частіше застосовуються зведення за Карпом або Куком.

Означення 15.2. Будь-яка мова програмування L₁ називається зводимою за Карпом до мови L₂, якщо існує функція F: [TEX]\sum_{}^{} [/TEX]*→[TEX]\sum_{}^{} [/TEX]*, що обчислюється за поліноміальний час, де F (x) належить L₂ в тому разі, якщо x належить L₁.

Розглянемо дві мови L₁ і L₂ над алфавітами [TEX]\sum [/TEX] і Г. Зведення L₁ до L₂ за Карпом - це функція f: [TEX]\sum [/TEX]*→Г*, обчислювана за поліноміальний час, така, що [TEX]\forall [/TEX]x[TEX]\in [/TEX]L₁ ↔ f(x) [TEX]\in [/TEX] L₂. Таким чином, неформально мова L₁ «не складніша» за мову L₂. Якщо така функція існує, кажуть, що L₁зводиться за Карпом до L₂, і пишуть L₁ ≤ _KL₂ . Відмітимо, що зведення за Карпом є частковим випадком зведення за Куком.

Означення 15.3. Зведення задачі R₁до задачі R₂ за Куком – це поліноміальний за часом алгоритм (іншими словами, машина Тюрінга з поліноміальним часом роботи), що розв’язує задачу R₁ за умови, що функція, що знаходить розв’язок задачі R₂, йому дана як оракул, тобто звернення до неї займає один крок.

Якщо такий алгоритм існує, кажуть, що R₁ зводима за Куком до R₂ і пишуть R₁ ≤ _CR_2.

Поява деяких нових класів складності пов’язана із залученням до процесу їх вивчення так званої «пророчої машини» - машини Тюрінга з оракулом. Пророк, у цьому розрізі, розглядається як сутність, здатна відповідати на набір питань і зазвичай представлена як деяка підмножина натуральних чисел. Тоді, інтуїтивно, пророча машина може виконувати всі звичайні дії машини Тюрінга і також може запитати у пророка: «Чи x належить A?».

Машина Тюрінга взаємодіє з оракулом шляхом запису на свій рядок вхідних даних для оракула і потім запускає оракул на виконання. За один крок оракул обчислює функцію, стирає вхідні дані й пише вихідні дані у рядок.

Клас складності задач, розв’язуваних алгоритмом з класу А з оракулом для задачі класу B, позначають A^B. Наприклад, клас задач, розв’язуваних за поліноміальний час детермінованою машиною Тюрінга з оракулом для NP-завдання, позначають P^NP.

Повернемося до одного з основних питань - яке ж практичне значення має вивчення теорії складності й класифікація завдань з точки зору NP-повноти (NPC)? Відповідь очевидна - часто набагато розумніше та ефективніше знайти доказ того, що розглянута задача належить до класу NPC, й відповідно до цього зайнятися пошуком досить точних наближених алгоритмів, ніж безрезультатно витрачати час на відшукання поліноміальних алгоритмів її розв’язання. Зрозуміло, що саме NPC-задачі відіграють тут центральну роль - справа в тому, що поліноміальний час є, хоча й першим, але досить гарним наближенням поняття «практичної можливості розв'язання задачі».

Нагадаємо, що задачі класу NPC відповідають двом умовам: по-перше, вони обов’язково належать класу NP; по-друге, будь-яка довільна задача з класу NP зводиться до цих задач. Якщо опустити першу умову, то одержимо клас задач NPH(non-deterministic polynomial-time hard) - клас задач, які "принаймні так складні, як найбільш важкі задачі в NP". Клас NPH містить у собі NPC (див. рис. 15.1), але виходить із меж класу NP( за гіпотези P ≠ NP). Серед задач NPC виділяють також задачі NPCS – NP- повні в сильному сенсі, як ті, що належать класу NP, є NP-повними та мають максимальне значення величин, що зустрічаються в цій задачі, обмежені зверху поліномом від довжини входу.

 

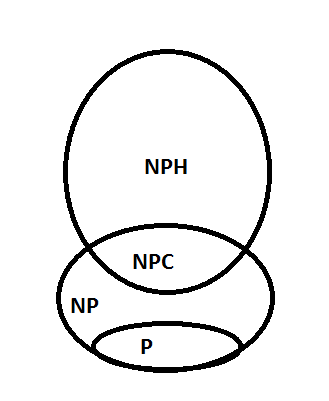
Рисунок 15.1 – Співвідношення між класами P, NP, NPC, NPH

 

15.1.2. Приклади NP-повних задач

Значення класу NP-повних проблем полягає ще й у тому, що йому належать дуже багато відомих і важливих у прикладному відношенні задач.

Проблемі доведення повноти цих задач присвячені дослідження багатьох видатних вчених з теорії алгоритмів. Будь-які доведення NP-повноти складні, але процедуру доведення можна спростити, застосувавши поняття зведення.

Для цього достатньо показати, що будь-яка з відомих NP-повних задач може бути зведена до цієї задачі.

Наприклад, Річард Карп у своїй праці «Зводимість між комбінаторними задачами» опублікував цілий список, що складається з формулювання та доведення NP-повноти 21 задачі. Перелічемо деякі з них.

1. Задача розбиття

Задана множина додатних цілих чисел x₁, x₂, ..., x_n. Чи можна розбити її на дві підмножини так, щоб суми чисел в обох підмножинах були однаковими?

2. Задача ізоморфізму підграфа

Нехай є два графи G₁ і G₂. Множину вершин першого графа позначимо V₁, а другого  V₂. Нехай | V1 |> | V2 |. Потрібно відповісти на запитання: чи знайдеться в графі G₁ підграф Н, ізоморфний графу G₂?

3. Задача виконуваності булевих формул (SAT).

Задача виконуваності булевих формул (SAT) важлива для теорії обчислювальної складності. Об'єктом задачі SAT є булева формула, що складається тільки з імен змінних, дужок та операцій (І), (АБО) і (HІ). Задача полягає в такому: чи можна призначити всім змінним, що зустрічаються у формулі, значення «ІСТИННІСТЬ» і «ХИБНІСТЬ» так, щоб формула набула значення «ІСТИННІСТЬ»?

4. Задача про кліку.

Маємо граф G з m вершинами і ціле додатне число n. Граф називається клікою, якщо кожна вершина в ньому зв'язана ребром з кожною. Кількість вершин у кліці назвемо її потужністю. Чи правда, що в даному графі G є кліка потужності не менше ніж n?

5. Задача про гамільтонів цикл.

Маємо граф G з n вершинами. Чи існує у графі простий цикл, що проходить через усі вершини графа? Простим називається цикл, у якому вершини не повторюються. Таким чином, гамільтонів цикл  це послідовність вершин і ребер (дуг) графа, що містить усі вершини графа G по одному разу, але щодо ребер обмежень не встановлено, то може бути, що містить не всі дуги.

6. Задача комівояжера.

Нехай є граф G з n вершинами. Кожному ребру графа приписано додатне ціле число d_i, що задає довжину ребра. Крім цього, задано деяке додатне ціле число L. Потрібно відповісти на запитання: чи знайдеться у графі G маршрут, що проходить через усі вершини графа G такий, що його довжина не перевищує L?

7. Вершинне покриття.

Задано граф G з m вершинами і ціле додатне число n. Вершинним покриттям називається підмножина U [TEX]\subseteq [/TEX] V множини V вершин графа така, що будь-яке ребро графа G інцидентне хоча б однієї з вершин множини U (друга вершина ребра може або належати, або не належати множині U). Чи існує вершинне покриття, що має в собі не більше ніж n вершин?

15.2. Алгоритмічно нерозв’язні проблеми

За час свого існування людство придумало безліч алгоритмів для вирішення різноманітних практичних і наукових проблем. Поставимо запитання: а чи існують такі проблеми, для яких неможливо придумати алгоритми їх вирішення?

Твердження про існування алгоритмічно нерозв'язних проблем є дуже переконливим, адже - ми констатуємо, що ми не знаємо відповідного алгоритму, не тільки зараз а й ми не можемо принципово ніколи його знайти. Виявляється, що існують такі класи задач, для розв’язання яких немає і не може бути єдиного універсального прийому. Проблеми розв’язання такого роду задач називають алгоритмічно нерозв'язними проблемами. Однак алгоритмічна нерозв'язність проблеми розв'язання задач того чи іншого класу зовсім не означає неможливість розв’язання будь-якої конкретної задачі з цього класу. Мова йде про неможливість вирішення всіх завдань даного класу одним і тим самим прийомом. Алгоритмічна нерозв'язність - найважливіша властивість деяких класів коректно поставлених завдань, що допускають застосування алгоритмів, яка полягає в тому, що задача кожного з цих класів у принципі не має загального, універсального алгоритму розв’язання, що об'єднує цей клас.

Алгоритмічна нерозв'язність не є проблемою теорії алгоритмів або невдачею, вона є науковим фактом. Популярність досліджень алгоритмічної нерозв'язності не поступається будь-яким іншим дослідженням у теорії алгоритмів і потребує іноді значних зусиль. Наприклад, доведення алгоритмічної нерозв'язності 10-ї проблеми Гільберта, одержане Ю. В. Матіясевичем, відносять до видатних наукових досягнень XX століття.

Знання можливої алгоритмічної нерозв’язності має в галузі комп’ютерних технологій таке саме значення, як для фізика знання про неможливість створення вічного двигуна. Припустимо, що до Білла Гейтса приходить винахідник з пропозицією надати йому грант (грошові інвестиції) для написання програми, яка приймає на вхід будь-яку програму і видає відповідь, потрапить ця програма в нескінченний цикл чи ні за будь-яких вхідних даних. Б. Гейтс йому, звісно, відповідь, оскільки знає, що ця задача є алгоритмічно нерозв'язною.

Означення 15.4. Алгоритмічною проблемою називається проблема побудови алгоритму, що володіє тими чи іншими властивостями.

Ми отримаємо вирішення алгоритмічної проблеми, якщо або знайдемо шуканий алгоритм (тобто подано його опис), або доведем, що такого алгоритму не існує.

Однією з найбільш загальних теорем теорії алгоритмів, що пояснює природу багатьох проблем у теорії алгоритмів, є теорема Райса.

Уведемо деякі визначення.

Означення 15.5. Характеристичною функцією множини А будемо називати функцію

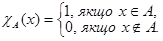                                                                                                                                                      (15.1)

Множина А називається рекурсивною, якщо її характеристична функція рекурсивна.

Означення 15.6. Нехай Q – деяка властивість одномісних частково-рекурсивних функцій. Властивість Q називається нетривіальною, якщо існують функції, що володіють цією властивістю, так і функції, що не володіють.

Усі властивості, що розглядаються в теорії алгоритмів, зазвичай є нетривіальними. Наприклад, властивості функцій : усюди визначеність, взаємна однозначність, тотожна рівна нулю та інші.

Ураховуючи те, що частково-рекурсивні функції можна задати програмою їх обчислення, виникає питання: чи можливо за програмою визначити, чи має відповідна функція певну нетривіальну властивість?

Відповідно до тез Черча і Тюрінга задача є алгоритмічно розв’язуваною тоді і тільки тоді, коли існує деяка машина Тюрінга М, що розв’язує цю задачу. За поставленим завданням необхідно визначити, чи характерна функції f_м(х), що реалізується машиною М, властивість Q. Функцію f_м(х) будемо розуміти як функцію, що відповідає програмі з номером Геделя x.

Теорема Райса. Якою б не була нетривіальна властивість Q одномісних частково-рекурсивних функцій, задача розпізнання цієї властивості алгоритмічно нерозв’язна, тобто не існує машини Тюрінга М,що розв’язує цю задачу.

Наслідки з теореми Райса. Неможливо за допомогою універсального алгоритму перевірити всюди визначеність функції f_м(х); не існує алгоритму перевірки того, що програма обчислить нульову функцію; питання про те, обчислюють чи ні дві програми одну й ту саму функцію, масово нерозв’язна; не існує алгоритму, що визначає за текстом програми, чи буде ця програма обчислювати деяку конкретну обчислювальну функцію.

Теорема Райса є однією з найбільш загальних теорем теорії алгоритмів, що пояснює природу багатьох проблем нерозв’язності у практиці програмування.

Першою фундаментальною теоретичною працею, пов'язаною з доведенням алгоритмічної нерозв'язності, була робота Курта Геделя  його відома теорема про неповноту символічних логік. Це була строго сформульована математична проблема, для якої не існує розв’язного її алгоритму. Зусиллями різних дослідників список алгоритмічно нерозв'язних проблем був значно розширений. Сьогодні прийнято під час доведення алгоритмічної нерозв'язності деякої проблеми зводити її до класичної задачі  «задачі зупину».

Теорема 15.3. Не існує алгоритму (машини Тюрінга), що дозволяє за описом довільного алгоритму і його вихідних даних (і алгоритм, і дані задані символами на рядку машини Тюрінга) визначити, зупиняється цей алгоритм на цих даних чи працює нескінченно.

Таким чином, фундаментально алгоритмічна нерозв'язність пов'язана з нескінченністю виконуваних алгоритмом дій, тобто неможливістю передбачити, що для будь-яких вихідних даних розв’язок буде отриманий за кінцеву кількість кроків. Тим не менше, можна спробувати сформулювати причини, що призводять до алгоритмічної нерозв'язності, ці причини достатньо умовні, оскільки всі вони зводяться до проблеми зупину, однак такий підхід дозволяє більш глибоко зрозуміти природу алгоритмічної нерозв'язності.

Приклад 15.1. Розподіл дев’яток у запису числа π

Визначимо функцію f (n) = i, де n - кількість дев'яток поспіль у десятковому записі числа π, а _i- номер найлівішої дев'ятки з n дев'яток поспіль:

π = 3,141592 ... f (1) = 5.

Завдання полягає в обчисленні функції f (n) для довільно заданого n.

Оскільки число π є ірраціональним і трансцендентним, то ми не знаємо жодної інформації про розподіл дев'яток (так само як і будь-яких інших цифр) у десятковому записі числа. Обчислення f (n) пов'язане з обчисленням наступних цифр у розкладанні, доти, поки ми не виявимо n дев'яток поспіль, однак у нас немає загального методу обчислення f (n), тому для деяких n обчислення можуть тривати нескінченно - ми навіть не знаємо в принципі (за природою числа π), чи існує розв’язок для всіх n.

Приклад 15.2. Десята проблема Гільберта

Вона полягає у знаходженні універсального методу цілочислового розв’язання довільного алгебраїчного діофантового рівняння. Доведення алгоритмічної нерозв'язності цієї задачі зайняло близько двадцяти років і було завершене Ю. В. Матіясевичем у 1970 році.

Формально мова йде про цілочислове розв’язання рівнянь вигляду

P (x₁, x₂,…, x_n) = 0, де P - многочлен із цілими коефіцієнтами й цілими показниками степенів. Доведено, що такого алгоритму не існує, тобто відсутній загальний метод визначення цілих коренів цього рівняння.