Модальна логіка
Термін “модальна логіка” виник в зв’язку з прагненням збагатити мову класичної логіки та розширити її можливості, додаючи в неї елементи, схожі на деякі часто вживані словесні конструкції. В цілому модальною логікою називають логічні системи, в яких використовуються оператори, подібні за змістом з модальними дієсловами природної мови: “можна”, “потрібно”, “можливо”, “неможливо”, “необхідно”, “обов'язково”, “дозволено”, “заборонено”, “впевнений”, “було”, “буде” та інші. В вузькому змісті, модальною логікою є логіка, в якій використовуються два основні оператори: [TEX]\Box [/TEX] - “обов'язково” (“необхідно”) й [TEX]\diamondsuit [/TEX]- “можливо”. Проте термін “модальна логіка” використовується більш широко, щоб покрити сімейство логік з аналогічними правилами. В принципі число груп модальних понять не обмежено, але модальні поняття різних типів мають загальні формальні властивості й визначаються друг через друга по одній і тій же схемі. Наприклад, основні оператори пов’язані між собою формулами:
[TEX]{\color{blue} {\Box A=\urcorner \diamondsuit \urcorner A}}[/TEX]. [TEX]\color{blue} {\diamondsuit A=\urcorner \Box \urcorner A}[/TEX] (6.1)
І цей взаємозв’язок цілком узгоджується зі звичайними уявленнями. Наприклад, фраза “Необхідно, що буде сьогодні дощ ” (ліва частина першої формули) відповідає фразі “Не можливо, що не буде сьогодні дощу” (права частина першої формули).
Перші дослідження в модальній логіці відносять до часів Аристотеля, й пов’язують з його ім’ям, та його учнів. До засновників сучасної модальної логіки відносять К. I. Льюїса та Я. Лукасевича, які в 1910-1932 роках ввели в сучасну логіку термін модальність. Третій період в становленні модальної логіки розпочато роботами С. А. Кріпке ( кінець 1950-х початок 60-х років) та продовжено дослідженнями К. Я. Ю. Хінтікка та Д. Льюїса.
Модальні логічні числення можна побудувати на основі числень класичної логіки (висловлювань та предикатів), шляхом розширення їх додатковими операторами, що характеризують ту чи іншу модальність. Наприклад, якщо оцінка того, що стверджується в висловлюваннях дається з позицій законів науки, то використовуються модальні оператори “необхідно”, “можливо”, якщо - з позицій пізнання, то - модальні оператори “доведено”, “ спростовано”, якщо - з позицій норм права, то – “обов'язково”, “дозволено”, “заборонено”, якщо - з позицій часу – “раніше”,”пізніше” та інші.
Логіки, сформовані на підставі того або іншого типу модальності, мають назви : "алетична логіка", "деонтична логіка", "епістемічна логіка", "часова логіка" та ін. (термін "логіка" використовують у цьому контексті як "теорія", "формально-логічна система").
Кожен тип модальності визначають з погляду об'єктивних (фактичних) і логічних детермінантів. Алетична модальність, зокрема, визначається з погляду об'єктивних законів природи, суспільства й логічних законів, деонтична модальність - з погляду прийнятних у суспільстві правових і моральних норм, епістемічна модальність - з погляду закономірностей пізнання об'єктивного світу, часова модальність - з погляду часових характеристик того, що відбувається в світі.
6.1. Особливості побудови модальних систем
Побудова формальної теорії в модальній логіці заснована на тих же засадах, що визначені для побудови будь-яких формальних аксіоматичних теорій (див. розділ 2.1) і включає в себе : а) введення алфавіту, що складається з пропозиційних символів , символів логічних та модальних зв’язків, символів дужок; б) визначення які слова з алфавіту є формулами; в) введення аксіом, як деякої підмножини формул; г) задання скінченої множини відношень між формулами, що називаються правилами виводу.
Означення 6.1.1. Модальною системою називається формально-логічна система (модель, теорія, числення модальних висловлювань), створена на підставі певного типу модальності засобами особливої мови на загальних принципах побудови логік.
У модальних системах виокремлюють немодальну частину та суто модальну частину. Немодальну частину представляє зазвичай класична математична логіка, а в модальній частині вводяться певного типу модальності та встановлюються логічні відношення між висловлюваннями з введеним типом модальності. Розрізняють семантику та синтаксис модальної логіки.
У семантичному аспекті визначають структуру модальних висловлювань на змістовному рівні. Це дає змогу виявити властивості висловлювань із певним типом модальності й виокремити онтологічні та логічні модальності, ввести терміни, що виокремлюють сферу міркувань з модальними висловлюваннями - висловлювання, властивість, відношення, терміни, які виокремлюють вид модальності - алетична, деонтична, епістемічна, часова та істиннісне значення висловлювання.
У синтаксичному аспекті структуру модальних висловлювань визначають абстрактно від їх змісту і формалізують засобами штучно створеної мови, на підставі чого здійснюють логічні операції над символами, що зображають логічні відношення між модальностями (числення модальностей).
Приклад 6.1.1. Наведемо опис модальної системи S1 К.І.Льюїса, побудованої за наведеними вище правилами.
Розв’язання. Вводимо алфавіт S, до якого входять : 1) p, q, r, … - символи для висловлювань; 2) [TEX]\urcorner, \vee, \wedge [/TEX] - символи логічних зв’язків; 3) [TEX]\Box ,\diamondsuit [/TEX] - символи модальних понять; 4 ), ( - дужки.
Визначаємо, що є формулами : 1) кожний з символів p, q, r, … є формулою; 2) якщо А та В є формулами, то наступні вирази теж є формулами:
¬ А – заперечення А; А [TEX]\vee [/TEX] В – диз’юнкція А і В; А [TEX]\wedge [/TEX] В – кон’юнкція А і В;
[TEX]\Box [/TEX]А – обов’язково А; [TEX]\diamondsuit [/TEX] А – можливо А; А→В = ¬ А [TEX]\vee [/TEX] В – матеріальна імплікація; А [TEX]\prec [/TEX] В = [TEX]\urcorner \diamondsuit (A\wedge (\urcorner B))[/TEX] – строга імплікація Льюїса; [TEX]A\leftrightarrow B=(A\rightarrow B)\wedge (B\rightarrow A)[/TEX] – матеріальна еквівалентність;A÷ В =[TEX](A\prec B)\wedge (B\prec A)[/TEX] – строга еквівалентність.
Вводимо аксіоми : А1)[TEX]p\wedge q\prec q\wedge p;A2)p\wedge q\prec p; A3)p\prec p\wedge p; A4)(p\wedge q)\wedge r\prec p\wedge (q\wedge r); A5)p\prec \urcorner (\urcorner p)[/TEX]; A6) [TEX](p\prec q)\wedge (q\prec p)\prec (p\prec q_; A7)p\wedge (p\prec q)\prec q[/TEX].
Визначаємо правила виводу : Р1. Правило заміни строго еквівалентним; Р2. Будь-які змінні p, q, r, … можна замінити довільними формулами; Р3. Введення кон’юнкції : із А, В виводиться А[TEX]\wedge [/TEX]В; Р4. Modus ponens зі строгою імплікацією: із А і А[TEX]\prec [/TEX]В виводиться В. Систему S1 побудовано.
Якщо додати до аксіом системи S1 аксіому А8) [TEX]\diamondsuit (p\wedge q)\prec \diamondsuit p[/TEX], то отримаємо систему S2. Взагалі Льюїсом були запропоновані й інші системи модальної логіки, наприклад S3-S5 й інші.
Відмітимо введення К. І. Льюїсом логіку поняття “строга іплікація” задля усунення парадоксів матеріальної іплікації. Відомо, що в матеріальній імплікації висловлювання А→В істинно в незалежності від В, якщо А - хибно. Чому, наприклад, з того, що 2x2=5 слідує, що Петров – студент? В строгій іплікації це вже виправлено.
Але не позбавлена парадоксів й строга імплікація. Для їх виключення Ф. В. Аккерман побудував свою систему модальної логіки. Серед відомих систем існують також системи Лукасевича та інші.
По відношенню до систем модальної логіки виникають ті ж проблеми, що мають місце в класичній логіці: проблема вирішення, проблема повноти та інші. Для систем Льюїса проблема вирішення розв’язується за допомогою алгебраїчних методів. С. А. Кріпке довів, що в численні одномісних предикатів з доданими модальними операторами проблема вирішення нерозв'язна. Цей результат дуже важливий, тому що він вказує на істотну відмінність модальної логіки від класичної математичної логіки. Доведена також неповнота числень Льюїса в тому сенсі, що в них виводима не всяка істинна формула.
Основною проблемою модальної логіки є те, що модальні оператори не являються істиннісне-функціональними, тобто істинність формули не є функцією от істинності її складових. Формула “[TEX]\diamondsuit [/TEX]p” може приймати значення істини, навіть якщо p є хибне, а формула “[TEX]\Box [/TEX]p” буде хибною, навіть якщо p є істинне. Для класичної логіки предикатів формальна семантика була створена, в той час як для модальної логіки її не існувало. Роботи Сола Кріпке дещо розв’язали ці проблеми й ввели нове поняття в модальну логіку – поняття можливого світу. Введення самого цього поняття в наукові праці приписують
Ґ. В. Лейбніцу, деякі джерела вказують, що поняття можливого світу в наукових дослідженнях з’явилося ще задовго до Лейбніца й повязують з філософом і теологом середньовіччя Й. Д. Скотом.
6.2. Семантика Кріпке
Серед відомих семантичних інтерпретацій модальних логік щонайчастіше застосовується семантика С. Кріпке (також відома як реляційна семантика або семантика фреймів), створена в кінці 1950-х і початку 1960-х років.
У моделі Кріпке задається множина можливих “світів” (станів), в яких може перебувати об'єкт, а також відношення досяжності на цій множині. При цьому модальний оператор “необхідно” інтерпретується як “істинно у всіх можливих досяжних світах”, а оператор “можливо” - як “істинно хоча б в одному з можливих досяжних світів”.
Означення 6.1.1. Фрейм Кріпке F або модальний фрейм представляє собою пару [TEX]\langle W,R\rangle [/TEX], де W є непорожньою множиною, а R є бінарним відношенням на W ( [TEX]R\subset W\times W[/TEX] ). Елементи множини W називають вузлами або можливими світами, а R - відношенням досяжності.
Означення 6.1.2. Моделлю Кріпке M називається пара [TEX]\langle F,\models \rangle [/TEX], де F - фрейм Кріпке, ![]() - є відношення між вузлами W і модальними формулами, такі, що:
- є відношення між вузлами W і модальними формулами, такі, що:
-
w
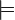 ¬ A тоді і тільки тоді w
¬ A тоді і тільки тоді w 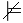 A;
A; -
w
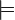 (A [TEX]\wedge [/TEX] B) тоді і тільки тоді w
(A [TEX]\wedge [/TEX] B) тоді і тільки тоді w 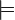 А і w
А і w 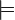 B;
B; -
w
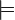 (A [TEX]\vee [/TEX] B) тоді і тільки тоді w
(A [TEX]\vee [/TEX] B) тоді і тільки тоді w 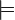 А або w
А або w 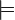 B;
B; -
w
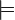 (A → B) тоді і тільки тоді w
(A → B) тоді і тільки тоді w 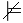 A або w
A або w 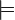 B;
B; 
-
w
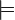 [TEX]\Box [/TEX] A тоді і тільки тоді [TEX]\forall u\in W[/TEX] якщо w R u, то u
[TEX]\Box [/TEX] A тоді і тільки тоді [TEX]\forall u\in W[/TEX] якщо w R u, то u 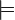 A;
A; -
w
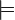 [TEX]\diamondsuit [/TEX] A тоді і тільки тоді [TEX]\exists u\in W[/TEX] виконується w R u і u
[TEX]\diamondsuit [/TEX] A тоді і тільки тоді [TEX]\exists u\in W[/TEX] виконується w R u і u 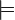 A.
A.
Позначення w ![]() A читаються так: “ w задовольняє А”, “ А виконується в w”.
A читаються так: “ w задовольняє А”, “ А виконується в w”.
У відповідності з цією семантикою, висловлювання р є необхідно-істинним по відношенню до можливого світу w[TEX]\in [/TEX]W, якщо воно істинне в кожному світі, досяжному для w, і р є можливо-істинним, якщо воно істинне в якомусь світі, досяжному для w. Можливість таким чином, залежить від відношення досяжності R, яке дозволяє висловити відносний характер можливості.
Введене в модель відношення досяжності R дозволяє вести класифікацію модальних логік , на предмет які властивості цих відношень підтримуються в тій чи іншій моделі. Наприклад, система модальної логіки К – не підтримує жодної властивості R; Т – логіка з R, що має властивість рефлексивності; S4 – підтримує рефлексивність та транзитивність R; S5 - підтримує еквівалентність R.
Формально ![]() можна уявити як деяку функцію (щонайчастіше її називають оцінкою), що приписує кожній формулі значення істинності по відношенню до кожного світу wW. Підсумком досліджень С. Кріпке стало те, що формули в модальній логіці будуть приймати значення істинності по відношенню до можливих світів.
можна уявити як деяку функцію (щонайчастіше її називають оцінкою), що приписує кожній формулі значення істинності по відношенню до кожного світу wW. Підсумком досліджень С. Кріпке стало те, що формули в модальній логіці будуть приймати значення істинності по відношенню до можливих світів.
Приклад 6.2.1. Представимо, що маємо висловлення p – “Лейбніц займався математикою”. Насправді, Г. В. Лейбніц займався математикою, тому p є істинним по відношенню до “нашого” актуального світу w1 [TEX]\in [/TEX] W. В даній моделі φ(p, w1) – “Істина”.
Цілком можливо, що Лейбніц не займався би математикою, а був би ювеліром. Отже, існує можливий світ w2 [TEX]\in [/TEX] W, в якому p та φ(p, w2) приймають значення “Хибність”.
Головна ідея такого аналізу в тому, що дозволяючи значенню істинності формул змінюватись від світу до світу, ми зможемо визначити їх значення істинності так, як це раніш було неможливим.
У логіці висловлювань атомарні висловлювання набувають значення істинності (І або Х), потім значення складних пропозицій (формул) розраховуються за таблицями істинності. У модальній логіці при введені семантики Кріпке спочатку вводиться набір W можливих світів. Потім надається значення істинності кожному висловлюванню для кожного з можливих світів в W. Це означає, що присвоєне висловлюванню р значення істинності для світу w1[TEX]\in [/TEX] W може відрізнятися від значення, присвоєного для іншого світу w2[TEX]\in [/TEX] W. Значення істинності атомарних р в світі w можна записати наступне φ(p, w). Враховуючи ці позначення, значення істинності (І для істинних, Х для хибних) складних речень (формул) модальної логіки визначається наступне:
-
φ(¬ А, w) = І тоді і тільки тоді φ( А, w) = Х;
-
φ(А→В, w) = І тоді і тільки тоді φ( А, w) = Х або φ(В, w) = І;
-
φ( [TEX]\Box [/TEX]А, w) = І тоді і тільки тоді [TEX]\forall u\in W[/TEX], φ(А, u) = І;
й тому подібне.
6.3. Теорія “двійників” К. Льюїса
Теорія “двійників” – альтернативна семантиці Кріпке інтерпретація модальної логіки з кванторами, запропонована Д. Льюїсом в 1968 році. Ідея полягала в тому, що модальні оператори не потрібні для квантифікації для можливих світів, тобто можна позбавитися від модальних операторів перетворивши звичайну модальну логіку в теорію “двійників”.
”Нова” теорія заснована на предикатах:
-
Wx (x є можливий світ);
-
Ipy (p знаходиться в можливому світі y);
-
Ap (p є актуальним індивідом);
-
Cqy ( q є двійником p).
Постулати теорії “двійників” наступні:
П1. Немає нічого за межами того, що є у можливому світі, можливі світи замкнуті; П2. Жодного індивіда не існує одночасно у двох можливих світах; П3. Чим би не був двійник, він знаходиться в якому-небудь можливому світі; П4. Те, у чого є двійник, знаходиться у можливому світі; П5. Ні у чого в можливому світі немає двійника в тому ж самому можливому світі, тобто жодний об’єкт в можливому світі неможна назвати двійником чого-небудь в тому ж можливому світі; П6. Будь-який об'єкт в можливому світі є власним двійником, єдиним двійником об’єкту в тому ж самому світі буде він саме; П7. Деякі можливі світи містять всі актуальні речі; П8. Щось є актуальне, тобто існує актуальний світ.
Приклад 6.3.1. Записати речення р звичайної мови “Могли б існувати літаючі люди” (що є аналогом питання “Чому люди не літають?”) за допомогою модальних операторів треба перевести його в мову теорії “двійників”.
Розв’язання. Спочатку переведемо вхідне речення р на мову, що використовує модальні оператори: р - “Можливо існує людина, що може літати”, що в модальній логіці представимо формулою
[TEX]\exists w\exists x(H(x)\wedge M(x))[/TEX] . (6.3.1)
В формулі (6.3.1) H(x) та M(x) є предикатами, побудованими на множині людей (Представте зміст предикатів самостійно).
В теорії “двійників” формула (6.3.1) набуде виду
[TEX]\exists w\exists x[/TEX] (w є можливий світ [TEX]\wedge [/TEX] х знаходиться в w [TEX]\wedge [/TEX] (H(x) [TEX]\wedge [/TEX]M(x)). (6.3.2)
Теорія “двійників” К. Льюїса є найбільш закінченою спробою звести поняття модальної логіки ([TEX]\Box ,\diamondsuit [/TEX]) до відношень подібності між конкретними сутностями, об’єктами в рамках понятійної моделі можливих світів.
Існують й інші семантики, що розглядають поняття модальної логіки з інших точок зору. Цікавою в цьому плані є теоретико-ігрова семантика
К. Я. Ю. Хінтікка, в основі якої знаходяться, з одного боку, математична теорія ігор, з іншого – теоретико-модальна семантика.



